Непрерывность функции на интервале и на отрезке

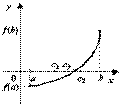
Рефераты / Математика / Непрерывность функции на интервале и на отрезке

Рис.3.16. Последовательные деления отрезка пополам

Получаем, что либо на некотором шаге будет найден корень , либо будет построена система вложенных отрезков

$\displaystyle [a;b]\sps[a_1;b_1]\sps[a_2;b_2]\sps\ldots\sps[a_i;b_i]\sps\ldots,$

в которой каждый следующий отрезок вдвое короче предыдущего. Последовательность $a_0=a,a_1,a_2,\dots,a_i,\dots$ - неубывающая и ограниченная сверху (например, числом ); следовательно (по теореме 2.13), она имеет предел $\lim\limits_{i\to\infty}a_i=a'$ . Последовательность ${b_0=b,b_1,b_2,\dots,b_i,\dots}$ - невозрастающая и ограниченная снизу (например, числом); значит, существует предел $\lim\limits_{i\to\infty}b_i=b'$ . Поскольку длины отрезков образуют убывающую геометрическую прогрессию (со знаменателем $\frac{1}{2}$ ), то они стремятся к 0, и $\lim\limits_{i\to\infty}a_i=\lim\limits_{i\to\infty}b_i$ , то есть . Положим, теперь . Тогда

$\displaystyle \lim_{i\to\infty}f(a_i)=f(a')=f(x_0)$ и $\displaystyle \lim_{i\to\infty}f(b_i)=f(b')=f(x_0),$

поскольку функция непрерывна. Однако, по построению последовательностей $\{a_i\}$ и $\{b_i\}$ , и , так что, по теореме о переходе к пределу в неравенстве (теорема 2.7), $\lim\limits_{i\to\infty}f(a_i)\leqslant 0$ и $\lim\limits_{i\to\infty}f(b_i)\geqslant 0$ , то есть $f(x_0)\leqslant 0$ и $f(x_0)\geqslant 0$ . Значит, , и - корень уравнения .

Пример 3.14 Рассмотрим функцию $f(x)=\cos x-x$ на отрезке $[0;\frac{\pi}{2}]$ . Поскольку и $f(\frac{\pi}{2})=-\frac{\pi}{2}$ - числа разных знаков, то функция обращается в 0 в некоторой точке интервала $(0;\frac{\pi}{2})$ . Это означает, что уравнение $\cos x=x$ имеет корень $x_0\in(0;\frac{\pi}{2})$ .

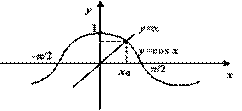
Рис.3.17. Графическое представление корня уравнения $\cos x=x$

Доказанная теорема фактически даёт нам способ нахождения корня , хотя бы приближённого, с любой заданной наперёд степенью точности. Это- метод деления отрезка пополам, описанный при доказательстве теоремы. Более подробно с этим и другими, более эффективными, способами приближённого нахождения корня мы познакомимся ниже, после того, как изучим понятие и свойства производной.

Заметим, что теорема не утверждает, что если её условия выполнены, то корень - единственный. Как показывает следующий рисунок, корней может быть и больше одного (на рисунке их 3).

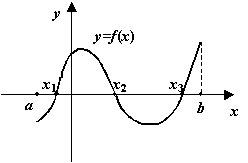
Рис.3.18. Несколько корней функции, принимающей значения разных знаков в концах отрезка

Однако, если функция монотонно возрастает или монотонно убывает на отрезке, в концах которого принимает значения разных знаков, то корень- единственный, так как строго монотонная функция каждое своё значение принимает ровно в одной точке, в том числе и значение 0.

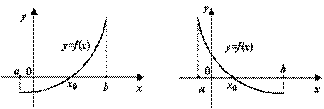
Рис.3.19.Монотонная функция не может иметь более одного корня

Непосредственным следствием теоремы о корне непрерывной функции является следующая теорема, которая и сама по себе имеет очень важное значение в математическом анализе.

Теорема 3.7 (о промежуточном значении непрерывной функции) Пусть функция непрерывна на отрезке и $f(a)\ne f(b)$ (будем для определённости считать, что ). Пусть - некоторое число, лежащее между и . Тогда существует такая точка $x_0\in(a;b)$ , что .