Непрерывность функции на интервале и на отрезке

Рефераты / Математика / Непрерывность функции на интервале и на отрезке

$\displaystyle \lim\limits_{i\to\infty}f(x_i)=\lim_{i\to\infty}K=K,$

а с другой стороны, вследствие непрерывности функции ,

$\displaystyle \lim\l<p>imits_{i\to\infty}f(x_i)=f(x_0).$

Значит, , так что точка принадлежит множеству и $x_0=\min M$ .

В случае, когда множество задано неравенством $f(x)\leqslant K$ , мы имеем $f(x_i)\leqslant K$ при всех $i=1,2,\dots$ и по теореме о переходе к пределу в неравенстве получаем

$\displaystyle \lim\limits_{i\to\infty}f(x_i)\leqslant K,$

откуда $f(x_0)\leqslant K$ , что означает, что $x_0\in M$ и $x_0=\min M$ . Точно так же в случае неравенства $f(x)\geqslant K$ переход к пределу в неравенстве даёт

$\displaystyle \lim\limits_{i\to\infty}f(x_i)\geqslant K,$

откуда $f(x_0)\geqslant K$ , $x_0\in M$ и $x_0=\min M$ .

Теорема 3.8 (об ограниченности непрерывной функции) Пусть функция непрерывна на отрезке . Тогда ограничена на , то есть существует такая постоянная , что $\vert f(x)\vert\leqslant K$ при всех $x\in[a;b]$ .

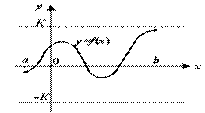
Рис.3.23. Непрерывная на отрезке функция ограничена

Доказательство. Предположим обратное: пусть не ограничена, например, сверху. Тогда все множества ${M_1=\{x\in[a;b]:f(x)\geqslant f(a)+1\}}$ , ${M_2=\{x\in[a;b]:f(x)\geqslant f(a)+2\},\dots}$ , ${M_i=\{x\in[a;b]:f(x)\geqslant f(a)+i\},\dots}$ , не пусты. По предыдущей лемме в каждом из этих множеств имеется наименьшее значение , $i=1,2,\dots$ . Покажем, что

$\displaystyle x_0=a<x_1<x_2<\dots<x_i<\dots.$

Действительно, . Если какая-либо точка из $x_2,x_3,\dots$ , например , лежит между и , то

$\displaystyle f(x_0)=f(a)<f(x_1)=f(a)+1<f(x_i)=f(a)+i,$

то есть - промежуточное значение между и . Значит, по теореме о промежуточном значении непрерывной функции, существует точка $x_*\in(x_0;x_i)$ , такая что , и $x_*\in M_1$ . Но , вопреки предположению о том, что - наименьшее значение из множества . Отсюда следует, что при всех $i\geqslant 2$ .

Точно так же далее доказывается, что при всех $i\geqslant 3$ , при всех $i\geqslant 4$ , ит.д. Итак, $\{x_i\}$ - возрастающая последовательность, ограниченная сверху числом . Поэтому существует $\lim\limits_{i\to\infty}x_i=x'$ . Из непрерывности функции следует, что существует $\lim\limits_{i\to\infty}f(x_i)=f(x')$ , но $f(x_i)=f(a)+i\to+\infty$ при $i\to\infty$ , так что предела не существует. Полученное противоречие доказывает, что функция ограничена сверху.