Линейное и нелинейное программирование

X = (2, 2, 1, 0, 0)

F’ = -6

F = -F’ = 6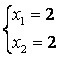

Задача № 2

Решаем задачу с x2 ≥ 3 в подсистеме «Поиск решения» системы Excel. Получаем допустимое не оптимальное решение F = 5, X = (1, 3)

2.3 Задача целочисленного линейного программирования с булевскими переменными

2.3.1 Постановка задачи целочисленного линейного программирования с булевскими переменными

Составить самостоятельно вариант для задачи целочисленного линейного программирования с булевскими переменными с учетом следующих правил: в задаче используется не менее 5 переменных, не менее 4 ограничений, коэффициенты ограничений и целевой функции выбираются произвольно, но таким образом, чтобы система ограничений была совместна. Задание состоит в том, чтобы решить ЗЦЛП с булевскими переменными, используя алгоритм Баллаша и определить снижение трудоемкости вычислений по отношению к решению задачи методом полного перебора.

 Скачать реферат