Линейное и нелинейное программирование
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
↕ |
&# 8597; |
↕ |
↕ |
↕ |
↕ |
|
y5 |
y6 |
y1 |
y2 |
y3 |
y4 |
|
2 |
4 |
7 |
0 |
0 |
5 |
F’ = Ф’ = 14
X = (2,4,7,0,0,5)
F= -F’ = -14 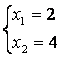
2.2 Задача целочисленного линейного программирования
2.2.1 Постановка задачи целочисленного линейного программирования
Решить ЗЦЛП, при условии целочисленности всех переменных, входящих в задачу, методом ветвей и границ и методом отсекающих плоскостей (методом Гомори).
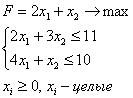
2.2.2 Метод Гомори
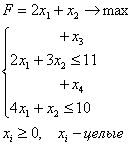
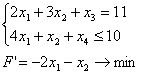
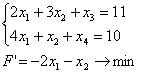
x3, x4 – базисные переменные, x1, x2 – свободные переменные
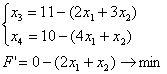
|
↑ | ||||||||
|
b |
x1 |
x2 | ||||||
|
x3 |
11 |
2 |
3 |
11/2 | ||||
|
-5 |
-1/2 |
-1/2 | ||||||
|
← |
x4 |
10 |
4 |
1 |
10/4 | |||
|
5/2 |
1/4 |
1/4 | ||||||
|
F’ |
0 |
2 |
1 | |||||
|
-5 |
-1/2 |
-1/2 | ||||||
|
↑ | ||||||||
|
b |
x4 |
x2 | ||||||
|
← |
x3 |
6 |
-1/2 |
5/2 |
12/5 | |||
|
12/5 |
-1/5 |
2/5 | ||||||
|
x1 |
5/2 |
1/4 |
1/4 |
10 | ||||
|
-3/5 |
1/20 |
-1/10 | ||||||
|
F’ |
-5 |
-1/2 |
1/2 | |||||
|
-6/5 |
1/10 |
-1/5 | ||||||
Другие рефераты на тему «Математика»:
Поиск рефератов
Loading
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
