Размерность конечных упорядоченных множеств

Возьмём любую цепь Z из множества цепей, пересечение которых образует решётку. Каждой такой цепи (а их ) во множестве цепей, пересечение которых образует множество, будет соответствовать своя цепь, все первые компоненты которой находятся в таком же соотве

тствии, как и элементы цепи Z .

Но во множестве среди вторых компонент должны сохраняться и соотношения, которые присутствуют в цепи В. Значит, во множестве цепей, пересечение которых образует множество , появится еще одна цепь.

Ч.т.д.

Теорема 4. решётка X, размерности n.

Доказательство:

Возьмём n не одноэлементных цепей А1, А2,…,Аn и рассмотрим множество X=A1A2… An=. (n-1) раз применяя теорему 3 получаем, что d(X)=n.

Ч.т.д.

Теорема 5.Размерность множества всех подмножеств ß(M) множества М равна мощности множества М, т.е.

d(ß(M))=.

Доказательство:

1) Покажем, что ß(M) @, где D={0,1}.

- будем рассматривать, как множество n-ок, состоящих из 0 и 1.

М={1,2,3,…,n}.

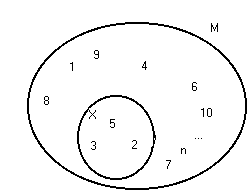
2) Чтобы доказать, что ß(M) и изоморфны, нужно установить взаимно однозначное соответствие.

Т.е. нужно показать, что для любого подмножества X множества М существует n-ка, состоящая из 0 и 1. И для любой n-ки существует подмножество Y множества М.

3) Выделим во множестве М подмножество X и составим по нему n-ку таким образом:

на место 1-ой компоненты n-ки поставим 1, если первый элемент множества М входит и в его подмножество X;

и 0, если 1-ый элемент множества М не входит в подмножество X.

Аналогичным образом определим все остальные компоненты n-ки.

Из нашего примера:

X (0,1,1,0,1,0…0)

n компонент

4) И, наоборот, возьмём произвольную n-ку. Например, (0,1,0,1,0…0). И поставим ей в соответствие подмножество Y множества М по тому же принципу:

если к-ая компонента равна 1, то к-ый элемент множества М входит в подмножество Y;

если же к-ая компонента равна 0, то к-ый элемент множества М не входит в подмножество Y.

Из примера получаем подмножество Y={2,4}.

5) Т.о. из ß(M)@следует, что d(ß(M))=d()n

Получили, что d(ß(M))=.

Ч.т.д.

Литература

1. Беран Л. Упорядоченные множества: Популярные лекции по математике. Вып. 55. – М.: Наука, 1981.

2. Биркгоф Г. Теория решёток. – М.: Наука, 1984.

3. Вечтомов Е. М. Теория решёток: учебно-методическая разработка спецкурса. – Киров: КГПИ, 1995.

4. Гретцер Г. Общая теория решёток. – М.: Мир, 1982.

5. Оре О. Теория графов. - М.: Наука, 1980.

 Скачать реферат