Размерность конечных упорядоченных множеств

(a,b)≤(c,d)Û(a≤c и b≤d).

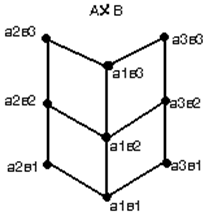
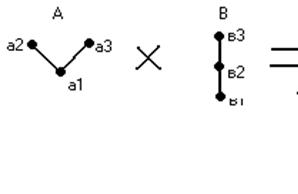
§2.Определение р

азмерности упорядоченного множества

Напомним, что такое цепь на примере диаграммы Хассе для конечного упорядоченного множества <A,£>. Здесь порядок £ будет линейным.

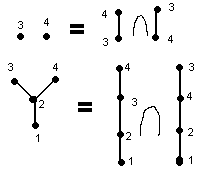
Примером антицепи может служить множество:

Нелинейный порядок £ на конечном упорядоченном множестве А можно доупорядочить до различных линейных порядков на А.

Например, нелинейный порядок на А

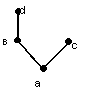
можно доупорядочить до следующих линейных порядков:

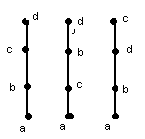
Для любого нелинейного порядка конечного упорядоченного множества будет справедлива теорема.

Теорема 1. Любой нелинейный порядок ≤ на конечном упорядоченном множестве А можно продолжить до линейных порядков, дающих в пересечении исходный порядок ≤.

Доказательство:

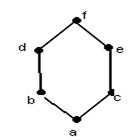
Возьмём произвольное конечное упорядоченное множество А с нелинейным порядком £.

Рассмотрим 2 его произвольных элемента а и b.

Если они несравнимы, то доопределим (или можно взять).

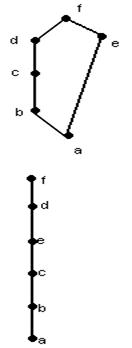Если при этом элемент x£ а, а элемент y ³ b, то .

В нашем примере b и с несравнимы. Доопределим . При этом, а £ b и c £ e, значит, .

Если <A,> - всё ещё не цепь, то, беря новую пару несравнимых элементов, аналогично доопределяем до “большего” порядка на А.

Через несколько таких шагов получим линейный порядок на A, содержащий исходный порядок £.

Если бы мы доопределили ba, тогда получили бы другой линейный порядок, содержащий исходный порядок £. В пересечении и í линейных порядков элементы a и b окажутся несравнимыми.

Аналогичным образом можно получить и другие линейные порядки, пересечение которых образует множество А.

Ч.т.д.

Из всего вышесказанного видно, что любой порядок на конечном упорядоченном множестве А является пересечением нескольких линейных порядков на А.

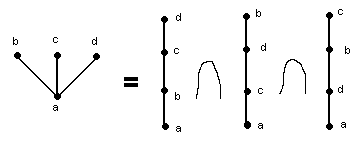
Наименьшее число линейных порядков на А, дающих в пересечении данный порядок £, называется размерностью А. И обозначается d(A).

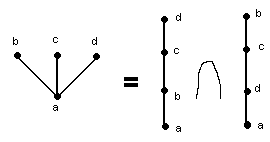
d(A)=2.

Корректность определения: каждое конечное упорядоченное множество имеет размерность. По определению конечного упорядоченного множества в нём будет конечное число элементов. А линейный порядок получается путём различных перестановок этих элементов. Если число элементов n, то число перестановок будет n! - конечное число. Из них выберем наименьшее число линейных порядков, пересечение которых даст исходное множество, и получим конечную размерность.

Цепи имеют размерность 1. Известно, что размерность всех множеств с количеством элементов n (где n£5), кроме цепей, равна 2.

Среди 6-элементных множеств существует только одно с размерностью 3.

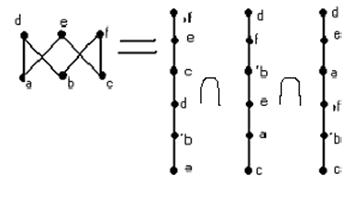
Остальные 6-элементные множества имеют размерность 2.

Дадим понятие перестановочно упорядоченного множества.

Пусть имеется множество А, состоящее из n элементов. А={1, 2 ,3 ,…, n}. Рассмотрим некоторую перестановку этого множества. (Например, (2, 1, 4, 3, …, n, n-1 )).

Эта перестановка задаёт свой линейный порядок на А, наряду с естественным числовым порядком, пересечение которых и определяет перестановочно упорядоченное множество < A, >.

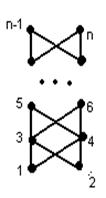
При этом, ав Û а<в и в данной перестановке n-ой степени число а встречается раньше числа в.

Конечные упорядоченные множества размерности 1 и 2 получаются с точностью до изоморфизма, как перестановочно упорядоченные множества.

Например, цепи Z: d(Z)=1

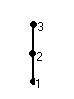
соответствует перестановка (1,2,3).

А множеству P: d(P)=2

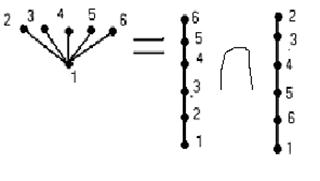
соответствует перестановка (1,6,5,4,3,2).

Перестановочно упорядоченные множества, отличные от цепей, - это в точности упорядоченные множества размерности 2.

Например, перестановка (5,3,1,2,6,4,7) задаёт упорядоченное множество размерности 2:

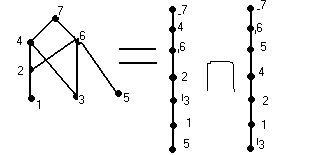
§3.Свойства размерности конечных упорядоченных множеств

Свойство монотонности: АÍВ Þ d(A) £ d(B) для любых конечных упорядоченного множества В и его непустого подмножества А.

Доказательство:

Пусть < B, ≤ >- конечное упорядоченное множество размерности n. Имеем, для линейных порядков £i на В. На подмножестве А рассмотрим индуцированный порядок из В, т.е. ограничение отношения £ на А.

Рассмотрим ограничения линейных порядков £i на А – они также линейны и в пересечении дадут порядок .

Значит, по определению размерности упорядоченного множества размерность <A, > не превосходит n.

Ч.т.д.

Свойство размерности дизъюнктивного объединения: Пусть А и В – конечные упорядоченные множества и X=AB. Тогда d(X)=max(d(A), d(B)), если хотя бы одно из множеств А или В не является цепью, и d(X)=2, если А и В – цепи.

 Скачать реферат