Размерность конечных упорядоченных множеств

Доказательство:

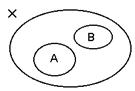Дизъюнктивным объединением упорядоченных множеств А и В (АВ) называется упорядоченное множество, состоящее из непересекающихся объединяемых множеств, на каждом из которых сохраняется свой порядок, а элемент

ы из разных множеств попарно несравнимы.

Пусть <A, £> и <B, > - конечные упорядоченные множества.

Порядок на А для линейных порядков £i , а порядок на В для линейных порядков .

Пусть для определённости n³m и n³2.

В результате объединения А и В получается упорядоченное множество, состоящее из всех элементов А и всех элементов В. Значит, одному линейному порядку на АВ соответствует два линейных порядка: один для А £i и один для В . Линейные порядки на АВ должны содержать все n линейных порядков £i и все m линейных порядков , чтобы в пересечении они дали множество АВ.

Первый линейный порядок на АВопределим следующим образом:

£1 … .

Т.е. мы взяли первый линейный порядок на А и приписали к нему справа первый линейный порядок на В.

Второй линейный порядок на АВполучим, взяв из множества А линейный порядок £2, а из множества В, если m³2, то линейный порядок , если же m=1, то линейный порядок . Но сейчас линейный порядок из множества А поместим за линейным порядком из множества В, для того, чтобы элементы из разных множеств были попарно несравнимы:

… £2, где j=1 при m=1 и j=2 при m³2.

Аналогичным образом будем получать остальные линейные порядки на АВ:

£i … при i£m

£i … при i>m.

Получим n линейных порядков, пересечение которых даёт множество АВ. Т.е. 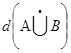=n=max(d(A), d(B)).

Ч.т.д.

Теорема 2. Размерность прямого произведения двух конечных упорядоченных множеств А и В меньше либо равна сумме их размерностей:

.

Доказательство:

Дадим сначала несколько определений.

Пусть даны конечные упорядоченные множества <А, £> и <В, £>, размерности которых соответственно равны m и n. Поэтому , для некоторых линейных порядков £i на А и для линейных порядков на В.

Определим покоординатно порядок на :

(a, b)<(c, d) Û (a < c и b £ d) или (a £ c и b < d).

Определим m линейных порядков на по первой компоненте:

(a, b)<i(c, d) Û a<i c или (a=c и b<1 d) для i=1,…,m. (*)

Аналогично определим n линейных порядков на по второй компоненте:

(a, b)<j(c, d) Û b<j d или (b=d и a<1 c) для j=1,…,n. (**)

Исходя из этих определений, порядок на можно определить и следующим образом:

(a, b)<(c, d)Û(a<ic и b£j d ) или (a£I c и b<j d) (***)

для i=1,…,m и для j=1,…,n.

Для завершения доказательства достаточно показать, что имеет место равенство:

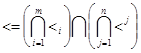
Тогда по определению размерности конечного упорядоченного множества получим .

Требуется доказать, что для любых (a,b) и (c,d) из :

(a, b)<(c, d) Û(a, b)<i(c, d) и (a, b)<j(c, d).

Для " (a,b) и (c,d) из не умоляя общности, будем считать, что

(a, b)<(c, d) (a<I c и b£j d) или (a£I c и b<j d) для i=1,…,m и для j=1,…,n.

Отсюда вследствие того, что x£y выполняется тогда и только тогда, когда x<y или x=y, следует равносильность:

Û(a<I c и b<j d) или (a<I c и b=d) или (a=c и b<j d)

для i=1,…,m и для j=1,…,n

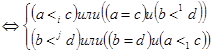
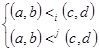
для i=1,…,m и для j=1,…,n.

Эта система равносильна тому, что элементы (a,b) и (c,d) сравнимы как по первой, так и по второй компоненте. И порядок на равен пересечению его линейных порядков.

А т.к. размерность – это наименьшее число линейных порядков, дающих в пересечении множество, то .

Ч.т.д.

Теорема 3. ЕслиА и В – не одноэлементные множества, причём А- решётка, а В –цепь, то размерность их прямого произведения на единицу больше размерности решётки:

.

Доказательство:

(по теореме 2).

Покажем, что выполняется и .

 Скачать реферат