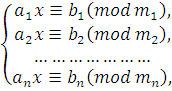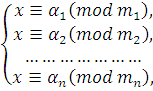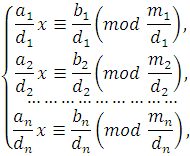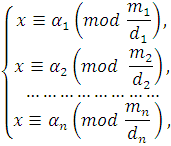Теория сравнений

Доказательство. Проведем индукцию по числу неизвестных . При утверждение теоремы верно. Предположим, что утверждение теоремы верно при , и возьмем произвольное тождественное сравнение 25 src="images/referats/3083/image550.png">, степень которого по каждому неизвестному меньше чем . Если наибольший показатель степени неизвестного , то сравнение можно представить в виде:

где все многочлены с целыми коэффициентами, степени которых по каждому неизвестному меньше чем . Если вместо подставить любые целые числа, то получим тождественное сравнение с неизвестной степени . Все коэффициенты этого сравнения: должны при любых значениях делиться на . Поскольку согласно предположению для многочленов от аргументов утверждение теоремы верно, все коэффициенты этих многочленов, а следовательно, и многочлена должны делиться на .

Согласно принципу полной математической индукции утверждение теоремы верно для любого числа аргументов.

4. Системы сравнений

4.1 Системы сравнений первой степени

Систему сравнений первой степени с одним и тем же неизвестным, но с разными модулями, запишем в общем виде так:

Общий способ (способ последовательного решения) состоит в том, что сначала находится из первого сравнения, где – наименьший неотрицательный или абсолютно наименьший вычет по модулю и берется класс чисел

удовлетворяющих первому сравнению.

Затем это значение подставляется во второе сравнение, что дает

откуда находится опять в виде класса чисел и подставляется в равенство (.

В результате получается значение в виде класса чисел, удовлетворяющих первым двум сравнениям системы. Дальше это значение подставляется в третье сравнение системы, так же находится , затем находится и подставляется в четвертое сравнение системы и т.д.

Заметим, что можно идти и несколько иным путем: сначала решается каждое из сравнений системы и представляется в виде:

а затем поступают описанным способом.

Если окажется, что хотя бы одно из сравнений системы (4.1) не имеет решения или сравнение относительно в описанном способе неразрешимо, то система (4.1) не имеет решения.

Если для сравнений системы (4.1) и то, сокращая члены и модуль каждого сравнения на получаем систему:

эквивалентную (4.1).

Сравнения этой системы можно решить относительно и свести решение системы (4.3) к решению системы:

Если в системе (4.2) модули попарно просты, то решение ее можно находить не указанным выше общим способом, а по формуле:

где и есть решения сравнений:

Решением системы будет:

Этим способом можно решать и систему (4.4), если модули попарно просты.

Пример 1. Решить систему сравнений:

Классы вычетов по : при имеем:

 Скачать реферат