Математическая модель в пространстве состояний линейного стационарного объекта управления
Если линейная стационарная система является полностью управляемой и наблюдаемой, то решение уравнения Риккати при ![]() стремится к установившемуся решению
стремится к установившемуся решению ![]() не зависящему от
не зависящему от ![]() и определяется следующим алгебраиче
и определяется следующим алгебраиче
ским уравнением:
![]()
В рассматриваемом случае весовые матрицы ![]() и
и ![]() в функционале не зависят от времени.
в функционале не зависят от времени.
Оптимальное значение функционала равно
![]()
и является квадратичной функцией от начальных значений отклонения вектора состояния.
Таким образом, получаем, что при ![]() оптимальное управление приобретает форму стационарной обратной связи по состоянию
оптимальное управление приобретает форму стационарной обратной связи по состоянию
![]()
где ![]() — решение алгебраического матричного уравнения Риккати.
— решение алгебраического матричного уравнения Риккати.
5.1.1. Решение алгебраического уравнения Риккати методом диагонализации
Для решения данной задачи найдем весовые матрицы ![]() и
и ![]() :
:
Выберем произвольно ![]() , тогда
, тогда
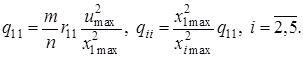
Взяв значения ![]() из решения задачи L – проблемы моментов получим:
из решения задачи L – проблемы моментов получим:

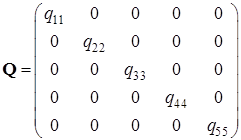
Матрицы системы имеют вид:
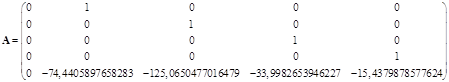
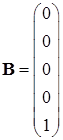 ,
, ![]() .
.
Введем расширенный вектор состояния 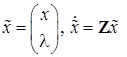 .
.
Тогда матрица Zбудет иметь следующий вид: 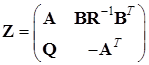 ,
,
или в численном виде
 .
.
Собственные значения матрицы ![]() :
:  .
.
Зная собственные значения и собственные вектора матрицы Z, построим матрицу ![]()
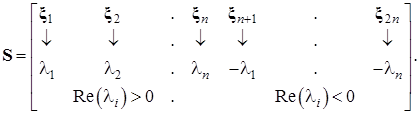
По определению все решения должны быть устойчивы при любых начальных условиях ![]() , т.е. при
, т.е. при ![]() . Чтобы не оперировать комплексными числами, осуществим следующий переход. Пусть:
. Чтобы не оперировать комплексными числами, осуществим следующий переход. Пусть:
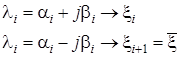
Тогда матрица ![]() формируется следующим образом:
формируется следующим образом:
 .
.
Можно показать, что матрицу можно получить из прямой матрицы собственных векторов:
 ,
,
![]() .
.
Установившееся решение уравнения Риккати, полученное с помощью скрипта Solve_Riccati_Method_Diag.m. имеет вид:
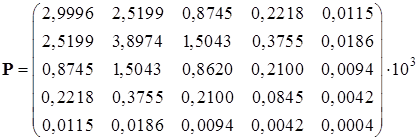
5.1.2 Решение алгебраического уравнения Риккати интегрированием в обратном времени до установившегося состояния
Весовые матрицы ![]() и
и ![]() такие же как и в пункте (5.1.1).
такие же как и в пункте (5.1.1).
Матрицы ![]() тоже аналогичны.
тоже аналогичны.
Запишем уравнение Риккати
![]() .
.
Зная, что ![]() , решаем уравнение методом обратного интегрирования на достаточно большом интервале (примерно 10 с.), получим установившееся решение с помощью скрипта
, решаем уравнение методом обратного интегрирования на достаточно большом интервале (примерно 10 с.), получим установившееся решение с помощью скрипта
Solve_Riccati_Method_Revers_Integr.m.:
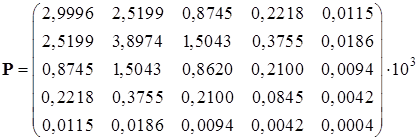
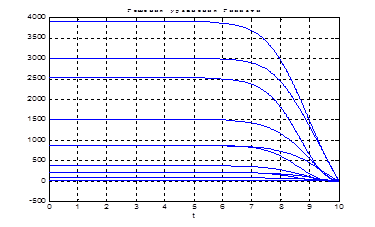
Рис.22. Графики решения уравнения Риккати.
Найдем разницу между решениями уравнения Риккати в пунктах 5.1.1 и 5.1.2:
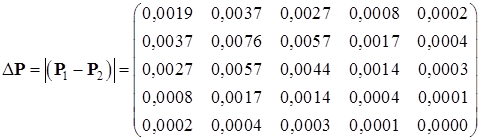
Выводы: сравнивая решения полученные в пунктах 5.1.1 и 5.1.2 можно сказать, что решения уравнения Риккати первым и вторым методами совпадают с заданной точностью. Погрешность расхождения решений невелика.
Используя скрипт AKOR_stabilizaciya_na_polybeskon_interval.m получим коэффициенты регулятора, фазовые координаты системы и управление.
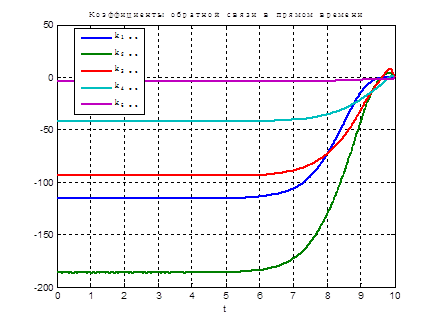
Рис.23. Графики коэффициентов регулятора обратной связи.
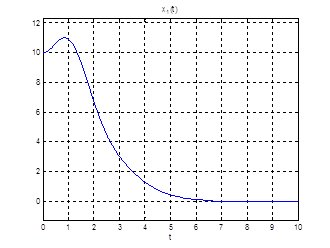
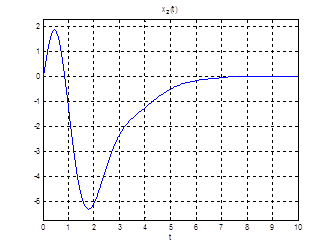
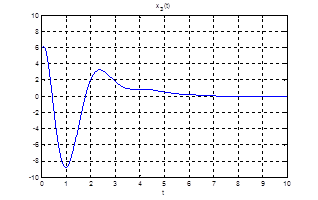
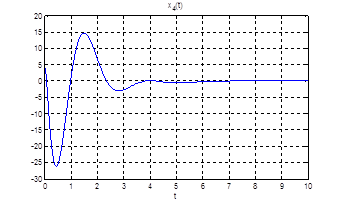
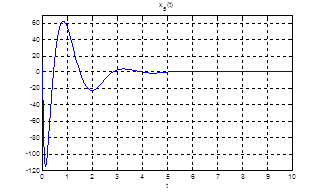
Рис.24. Графики фазовых координат.
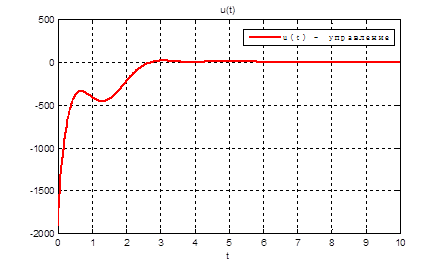
Рис.25. График управления.
Выводы: т.к. решения уравнения Риккати методом диагонализации и интегрирования в обратном времени дают практически одинаковый результат, то можно считать, что задача АКОР – стабилизации на полубесконечном интервале решена с заданной точностью.
5.2 Стабилизации объекта управления на конечном интервале времени
Рассмотрим линейный объект управления, описываемый системой дифференциальных уравнений в нормальной форме
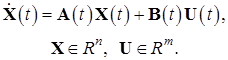
Начальные условия для заданной системы ![]()
Время стабилизации ![]() .
.
Необходимо получить закон управления
![]()
минимизирующий функционал вида
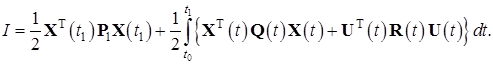
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
- Выборочные исследования в эконометрике
- Временные характеристики и функция времени. Графическое представление частотных характеристик
- Автоматизированный априорный анализ статистической совокупности в среде MS Excel
- Биматричные игры. Поиск равновесных ситуаций
- Анализ рядов распределения
- Анализ состояния финансовых рынков на основе методов нелинейной динамики
- Безработица - основные определения и измерение. Потоки, запасы, утечки, инъекции в модели
