Численные методы

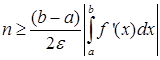. (24)

Для кусочно-непрерывной f’(x) с учётом (20) и (21) справедливо следующее

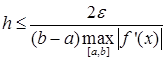(25)

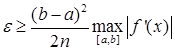
src="images/referats/11778/image049.png"> (26)

Метод правых прямоугольников

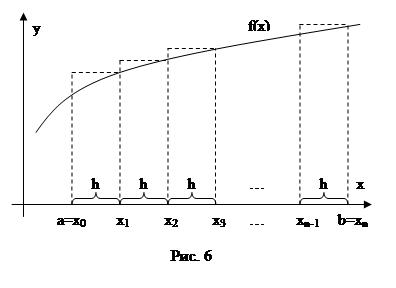
Этот метод похож на предыдущиу. Отличие в том, что высота прямоугольников вычисляется по правой границе (Рис. 6).

Выводы формул для данного метода аналогичны предыдущему. Основные отличия заключаются в нумерации. Формула метода правых прямоугольников выглядит следующим образом:

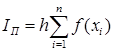. (27)

Рассуждения и конечные формулы, связанные с определением погрешности метода и выбором ширины основания прямоугольников аналогичны тому, что получено в предыдущем методе.

Метод средних прямоугольников

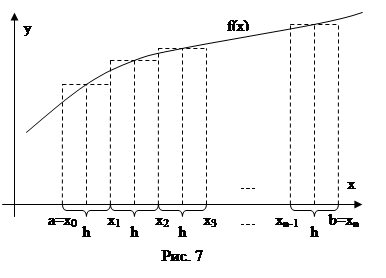
Чтобы уменьшить погрешность методов левых и правых прямоугольников был предложен метод средних, т.е. метод в котором высота прямоугольника вычисляется в середине отрезка h (Рис. 7). Обращаясь к рисунку легко увидеть, что площади прямоугольников вычисляются по следующим формулам:

(28)

Оценим погрешность формулы (28) на отрезке [xi,xi+h]. Прежде всего, получим разложение по формуле Тейлора для данного метода. Центр разложения в данном случае будет точка . Тогда получим:

(29)

В формуле (29) отбросим члены, содержащие 3-ю и выше производные. Получаем:

Ii-IСр.i=RСр.i

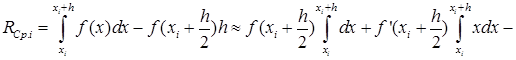
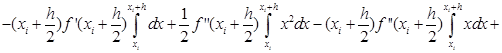
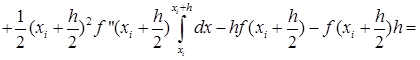
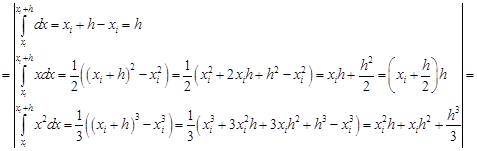
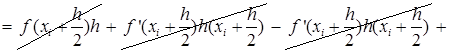
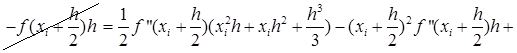
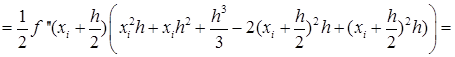
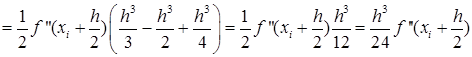, т.е.

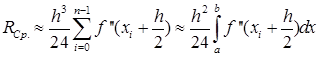. (30)

Аналогично тому, как были получены формулы (20), (21), (23), (24), (25) можно получить формулы, по которым оцениваются n и h, для данного метода. Запишем окончательные формулы для непрерывной f’’(x).

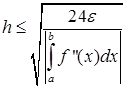(31)

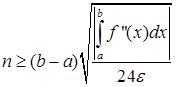(32)

Для кусочно-непрерывной f’’(x) получаем мажорантные оценки:

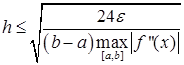(33)

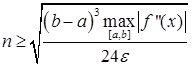(34)

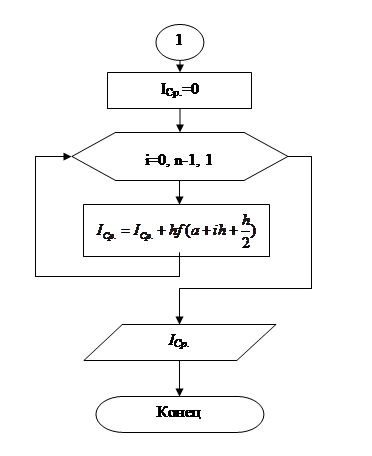
Сравнивая формулы (19) и (30) погрешностей методов приходим к выводу, что погрешность метода средних во много раз ниже погрешности метода левых или правых прямоугольников, т.е. метод средних во много раз точнее и для достижения заданной точности требует меньше машинного времени. Поэтому блок-схему построим именно для метода средних.

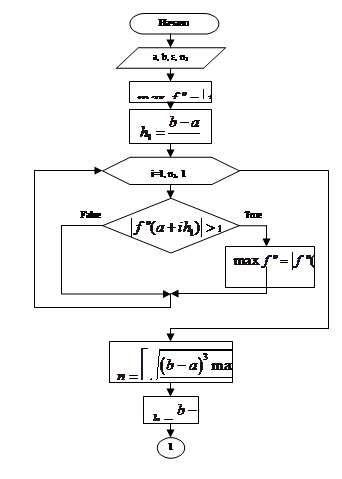
Введём обозначение. [n] – целая часть n, полученная путём отбрасывания дробно части. Для вычисления интеграла дано ε, [a,b], f(x), f’’(x). Прежде всего, через ε необходимо получить n. Пользоваться формулой (32) мы не будем, т.к. в ней необходимо вычислять интеграл. Воспользуемся мажорантной оценкой (34). Для этого перед вычислением интеграла необходимо найти , но это легко осуществимо с помощью небольшого циклического процесса. Для него понадобиться знание количества разбиений , на которых будем вычислять значения второй производной. Обозначим это количество n1.

Метод трапеций

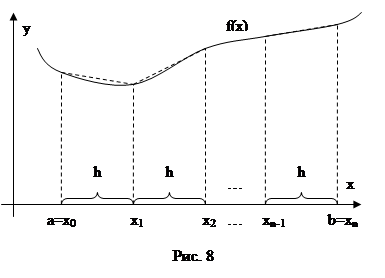
Метод трапеций основан на том, что криволинейная трапеция приближается прямолинейной (Рис. 8). Т.е. площади вычисляются по следующей формуле:

Таким образом, получаем общую формулу трапеций:

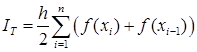. (35)

Теперь оценим погрешность метода. Вывод формулы погрешности аналогичен выводу (30), поэтому приведём сразу окончательную оценку погрешности для непрерывной f’’(x):

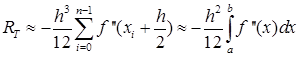; (36)

для кусочно-непрерывной f’’(x):

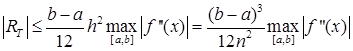(37)

Оценивая n и h, получим:

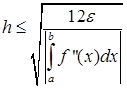(38)

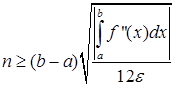(39)

Для кусочно-непрерывной f’’(x):

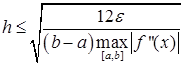(40)

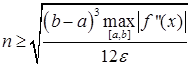(41)

Как видно из полученных формул погрешность метода средних примерно вдвое меньше погрешности метода трапеций. Очевидно, что если функция определена на всём интервале, лучше пользоваться методом средних, метод трапеций используют обычно для функций определённых только в узлах сетки. Знаки главного члена погрешности у формул трапеций и средних разные. Поэтому, если есть расчёты по обеим формулам, то точное значение интервала лежит, как правило, в вилке между ними. Деление этой вилки как 2:1 даёт уточнённый результат близкий к тому, который получается при использовании более точного метода Симпсона.

Метод Симпсона

Этот метод основан на том, что функция f(x) приближается на отрезке [xi-h, xi+h] параболой (причём xi отстоит от xi+1 на расстоянии 2h) (Рис.9). То есть через заданные точки проводится парабола. Но известно, что уравнение параболы имеет вид ρ(x)=ax2+bx+c, т.е. чтобы определить коэффициенты a, b, c необходимо решить систему из трёх уравнений, а для этого необходимо знать координаты как минимум трёх точек, через которые проходит парабола ρ(x). В связи с этим, в отличие от предыдущих методов, для вычисления площади отдельной криволинейной трапеции понадобиться не две, а три точки. Для вывода формулы Симпсона рассмотрим подробнее i-ю криволинейную трапецию ограниченную сверху параболой ρi(x).

 Скачать реферат