Теория вероятности

Задание 1

Общее число возможных элементарных методов равно числу сочетаний из 10 по 5:

.

Подсчитываем число исходов, благоприятствующих нашему событию. Среди 3-х женщин две женщины могут быть выбраны способами; при этом остальные 5–2

=3 людей должны быть мужчинами. Взять же 3 мужчины из 7 можно способами. Следовательно, число исходов благоприятствующих нашему событию:

.

Искомая вероятность равна:

.

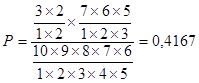Задание 2

.

Возможны следующие три случая:

А – среди трех студентов посетивших библиотеку первый заказал учебник по теории вероятностей, а два других не заказали;

В – второй студент заказал учебник по теории вероятностей, а первый и второй нет.

Вероятность каждого из этих событий по теореме умножения равны:

;

;

.

Искомая вероятность по теореме сложения несовместных событий:

.

Поэтому: .

Чтобы нити оказались одного цвета должны выполниться следующие события:

А – вынуть две нити красного цвета;

В – вынуть две нити белого цвета.

Вероятность каждого из этих событий по теореме умножения вероятностей будут:

;

.

Искомая вероятность по теореме сложения вероятностей: .

Задание 3

.

I – 4б; 6кр; II – 5б; 10кр

Обозначим события А – выбранный шар белый. Можно сделать два предложения:

– белый шар выбран из 1-го ящика

– белый шар выбран из 2-го ящика, так как ящик выбирают на удачу, то:

.

Условная вероятность того, что шар будет белым и извлечен он из первого ящика будет:

.

Вероятность того, что белый шар будет извлечен из второго ящика:

.

Формула полной вероятности:

.

Тогда вероятность того, что наугад взятый шар будет белым:

.

Задание 4

Воспользуемся локальной теоремой Лапласа:

;

;

.

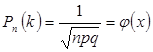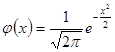В нашем случае n=600; k=25; P=0,05; q=0,95.

.

Так как функция – четная, то по таблице находим:

.

Тогда .

Задание 5

.

;

;

;

.

Начальный момент первого порядка: .

Аналогично: .

.

Находим центральные моменты по формулам:

;

;

.

Следовательно:

; ; .

Многоугольник распределения

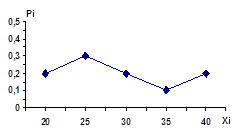
Задание 6

Распределение Х и распределение Y

;

.

;

;

;

;

;

.

Коэффициент коррекции находим по формуле:

,

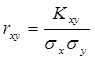где: Kxy – корелляционный момент связи случайных величин X и Y; – среднеквадратические отклонения величин X и Y.

 Скачать реферат