Численные методы

В силу утверждения 1 будем рассматривать только корни нечётной кратности. Так как функция меняет знак на концах отрезка, предположим, f(a)≥0, f(b)≤0. Тогда если f(xc)≥0, то для дальнейшего приближения выберем отрезок [xc,b], т.к. f(b)f(xc)≤0. Если же f(xc)≤0, то для дальнейшего приближения выберем отрезок [a,xc], т.к. f(a)f(xc)≤0.Для второго случая, когда f(a

)≤0, f(b)≥0 аналогично доказывается существование одного из полуотрезков, на котором функция меняет знак. Из чего следует, что после каждой итерации для одного из полуотрезков условие смены знака обязательно будет выполнено. Следовательно, нет причин для остановки итерационного процесса, который завершится лишь по достижении заданной точности.

Построим блок-схему алгоритма вычисления корня уравнения вида (1) с помощью метода дихотомии. Пусть на начальном отрезке [a,b] функция меняет знак, т.е. на этом отрезке существует нечётное количество нечётно кратных корней. Пример такой функции изображён на рис. 1. Необходимо найти корень xт с точностью ε. Будем считать xт точным значением корня, xч – значение корня полученное данным методом, тогда задача считается выполненной, если xчÎ[xт-ε,xт+ε].

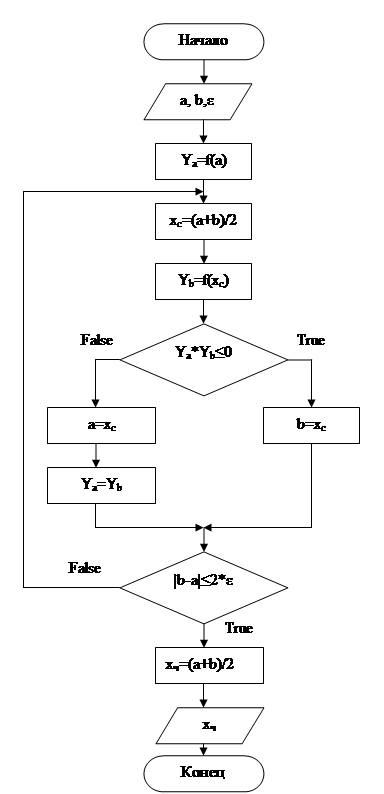
Дихотомия применяется тогда, когда требуется высокая надежность счета, а скорость сходимости малосущественна.

Метод простых итераций

Основной принцип метода заключается в том, что уравнение (1) представляется в виде:

x=φ(x), (4)

где φ(x) можно определить многими способами, например, так:

φ(x)=x-αf(x), α=const, или

φ(x)=x+ψ(x)f(x),

где ψ(x) – произвольная, непрерывная, знакопостоянная функция на отрезке [a,b].

Метод простых итераций в силу (4) определяется следующей рекурсивной формулой:

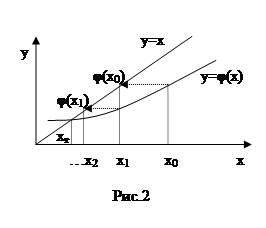
xn+1=φ(xn), где n=0,1,2,… (5)

Здесь n имеет смысл номера итерации, x0 – некоторое начальное приближение. Из (5) видно, что если xn→xт, то этот предел и есть корень уравнения (рис. 2).

Пусть в окрестности точки xт (xт-Δ,xт+Δ), где Δ>0 функция φ(x) удовлетворяет условию Липшица:

|φ(x2)-φ(x1)|≤q|x2-x1| (6)

для любых x2,x1Î(xт-Δ,xт+Δ),

0<q<1, (7)

при этом x0Î(xт-Δ,xт+Δ), (8)

причём, (xт-Δ,xт+Δ) Î[a,b].

В связи с этим допущением можно сделать несколько утверждений.

Утверждение 1.

Полученные с помощью (5) xnÎ(xт-Δ,xт+Δ) для любого целого n≥0.

Доказательство

В силу (8)

|x0-xт|<Δ,

из (5),(6) и (7) получим

|x1-xт|=|φ(x0)-φ(xт)|≤q|x0-xт|,

|x2-xт|=|φ(x1)-φ(xт)|≤q|x1-xт|≤q2| x0-xт|,

|xn-xт|=|φ(xn-1)-φ(xт)|≤q|xn-1-xт|≤q2| xn-2-xт|≤…≤ qn| x0-xт|<Δ, (9)

Из последнего неравенства |xn-xт|<Δ следует, что для любого целого n≥0 верно утверждение 1.

Утверждение 2.

Последовательность {xn} сходится при n→∞ к пределу xт, являющемуся корнем уравнения.

Доказательство.

В силу (5) и (6):

|xn+m-xn|=|φ(xn+m-1)-φ(xn-1)|≤q|xn+m-1-xn-1|≤q2|xn+m-2-xn-2|≤…≤qn|xm-x0| (10)

Следовательно, в силу (7) для любого целого

m≥0

Значит в силу признака Коши* предел существует . Докажем теперь, что xlim=xт. Из (10) следует (для определённости возьмём m=1), что , т.е. при n→∞ xlim=xn+1=xn, а в силу (5) xn+1=φ(xn) => xlim=xn=φ(xn) => xlim=φ(xlim). Из этого равенства следует, что xlim есть корень уравнения (4), т.е. xlim=xт.

Утверждение 3.

На интервале (xт-Δ,xт+Δ) существует только 1 корень уравнения (2).

Доказательство.

Пусть существует 2 корня

x1 и x2≠x1, тогда в силу (4) x1=φ(x1), x2=φ(x2).

Из (6) следует |x2-x1|=|φ(x2)-φ(x1)|≤q|x2-x1|, т.е. |x2-x1|≤q|x2-x1|.

Из этого следует, что q=1, а это противоречит (7). Следовательно, корень только 1.

Следует так же отметить, что если φ(x) имеет на интервале (xт-Δ,xт+Δ) непрерывную производную, то (6) выполняется, когда

|φ′(x)|≤q => |φ′(x)|<1 для xÎ(xт-Δ,xт+Δ). (11)

Если |φ′(xт)|<1, x0Î(xт-Δ,xт+Δ), то итерации сойдутся.

Если |φ′(xт)|>1, то в силу непрерывности производной |φ′(x)|>1 и на некотором интервале (xт-Δ1,xт+Δ1), поэтому итерации не сойдутся к корню. Если же |φ′(xт)|<1, но x0Ï(xт-Δ,xт+Δ), т.е. |φ′(x0)|>1, то в данном случае о сходимости процесса можно судить только после дополнительного анализа функции φ(x).

Как и при поиске решения методом дихотомии будем считать задачу выполненной, если найденное некоторое значение xчÎ[xт-ε,xт+ε], где ε – заданная точность. Для определения того, когда можно прекратить итерации, т.е. когда достигнута заданная точность, подробнее рассмотрим неравенство (9). По сути, нам необходимо добиться выполнения следующего неравенства:

|xn+1-xт| ≤ ε, (12)

а в силу того, что из (9) можно получить неравенство

|xn+1-xт| ≤ qn+1|x0-xт|,

где q можно определить как 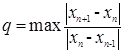для любого целого n≥1, выведем условие достижения заданной точности (12). Введём обозначения

δn+1=|xn+1-xт|. Из (9) ,

а так же очевидно, что δ0-δn+1=|x0-xn+1|=ξ, тогда:

δ0=δn+1+ξ

δn+1=gδ=g(δn+1+ξ)

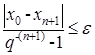. (13)

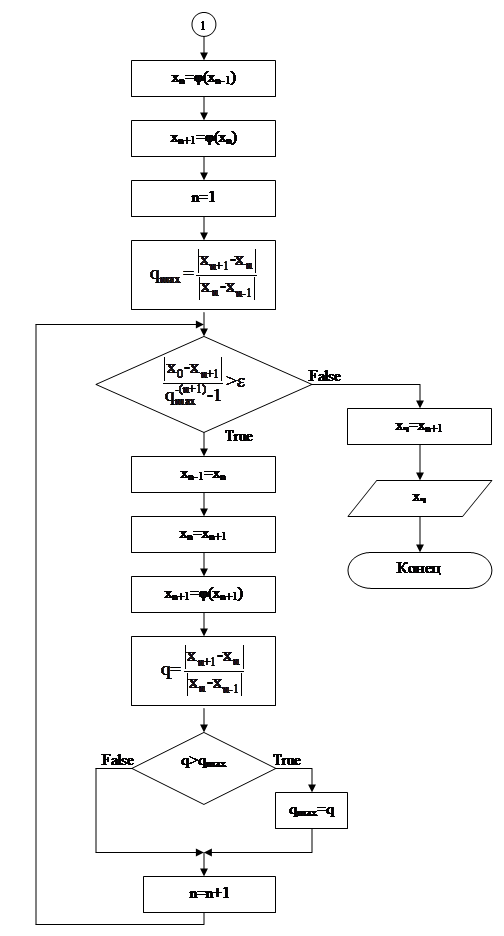
Неравенство (13) является условием остановки процесса итераций, т.е. условием достижения заданной точности. В завершение рассмотрения данного метода остаётся только построить блок-схему его алгоритма. Будем считать, что |φ′(xт)|<1, x0Î(xт-Δ,xт+Δ).

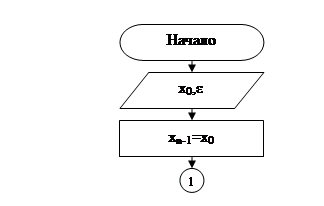
Метод касательных (Ньютона)

Метод Ньютона называют также методом касательных и методом линеаризации. Суть метода заключается в том, что в точке приближения к функции строится касательная (Рис. 3). Следующая точка приближения – это точка пересечения полученной прямой с осью Ox. Процесс продолжается вплоть до достижения заданной точности.

 Скачать реферат