Численные методы

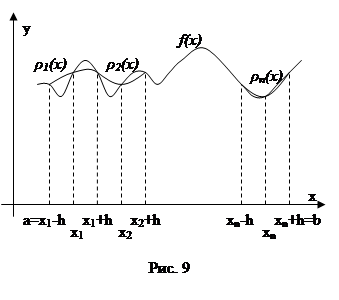
Для упрощения расчётов сделаем следующие преобразования. Перенесём i-ю криволинейную трапецию в начало координат так, что xi=0 (следовательно, xi-h=-h, xi+h=h). Очевидно, что её площадь не изменится. Найдём её площадь (Рис. 10). Для нахождения площади кривол

инейной трапеции необходимо знать форму кривой ограничивающей её. В нашем случае это парабола . Для нахождения коэффициентов ai, bi, ci составим систему из трёх уравнений. Для простоты обозначим

ai≡a, bi≡b, ci≡c, f(xi-h)≡f0, f(xi)≡f1, f(xi+h)≡f1.

Тогда

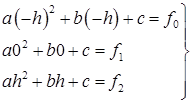
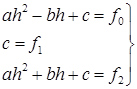
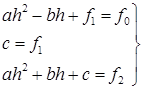
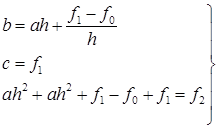
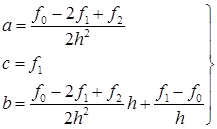
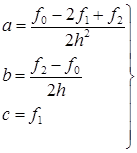
Таким образом, получаем

. (42)

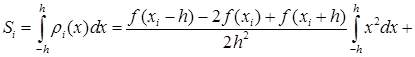
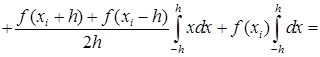
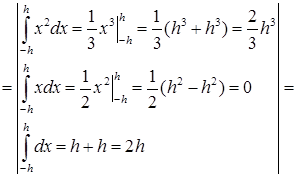
. (43)

Таким образом, получаем общую формулу Симпсона:

Для упрощения этой формулы учтём, что

, , ,

где a и b – границы отрезка интегрирования [a, b]. С учётом этого получим:

,

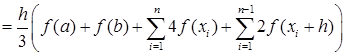где n – количество отрезков длиною 2h. То есть количество отрезков h, на которые разбит отрезок [a, b] должно быть обязательно чётным. Длина отрезка [a, b] равна 2nh.

Для оценки погрешности формулы Симпсона на отрезке [xi-h, xi+h] разложим функцию f(x) по формуле Тейлора до пятого члена с центром разложения в точке xi. То есть

(44)

Тогда с учётом (43) и (44) получим:

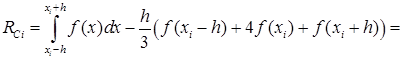
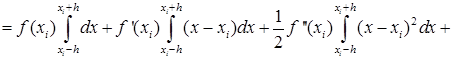
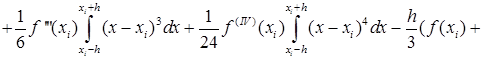
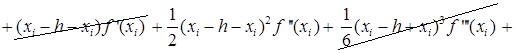
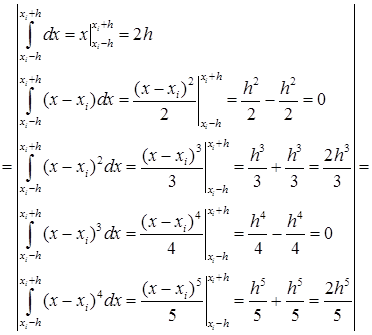
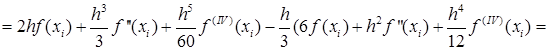
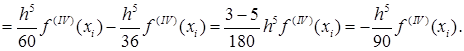
Т.е.

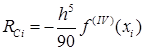
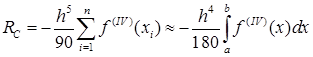, (45)

Сравнив формулы (45), (36), (30) и (19) увидим, что метод Симпсона является наиболее точным из всех описанных методов численного интегрирования.

Учитывая, что для метода Симпсона , запишем формулы оценки n и h для заданного ε. Для непрерывной :

,

.

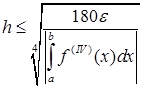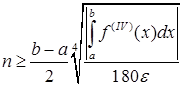Мажорантные оценки для кусочно-непрерывной :

,

.

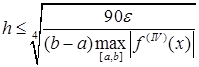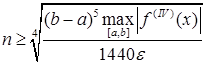Построим блок-схему.

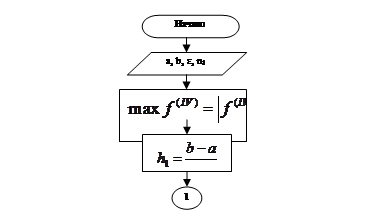
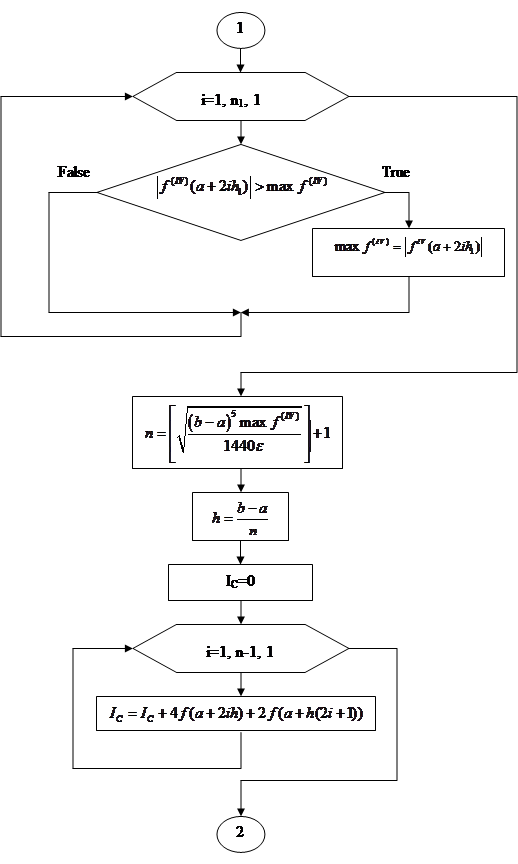
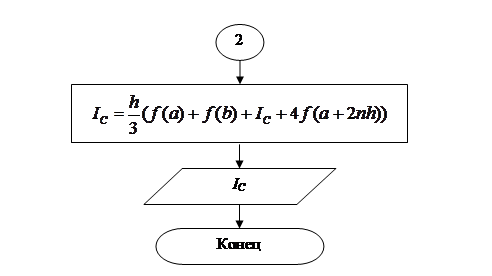
Приближение функций

Как известно, функцию можно задать многими способами. Самые распространённые из них – это аналитический, графический и табличный. В первых двух способах функция обычно определена на бесконечном числе точек, третий же способ задаёт лишь их конечное количество, например, экспериментальные данные или результаты сложных вычислений. В связи с этим встаёт вопрос получения промежуточных значений таблично заданной функции. Для их нахождения используют два способа: интерполяция (экстраполяция)* и аппроксимация. При использовании интерполяции считают табличные значения точными и интерполяционный многочлен должен точно проходить через заданные точки (Рис. 11). Аппроксимирующая же функция лишь приближается как можно ближе к заданным точкам, но не обязательно через них проходит (Рис. 13). Это связано с тем, что табличные данные считаются приближенными, и точное прохождение функции через эти точки будет только увеличивать ошибку.

Интерполяция

Итак, как было сказано выше, задачей интерполяции является поиск такого многочлена, график которого проходит через заданные точки.

Пусть функция y=f(x) задана с помощью таблицы (табл. 1).

Таблица 1

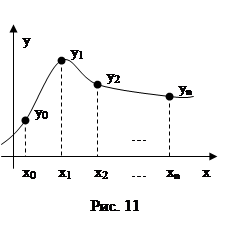
Необходимо получить многочлен Pn(x) такой, чтобы выполнялось условие:

Pn(xi)=yi. (46)

Для этого зададимся конкретным видом многочлена. Пусть Pn(x) имеет следующий вид:

Pn(xi)=a0+a1x+a2x2+…+anxn. (47)

Для того, чтобы определить коэффициенты a0, a1,… необходимо решить систему из n уравнений с n неизвестными:

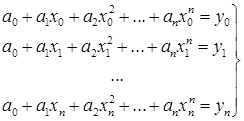(48)

Полином с коэффициентами, полученными путём решения системы (48) называют интерполяционным полиномом Лагранжа и обозначают Ln(x). Решение системы (48) весьма трудоёмко, поэтому интерполяционный полином Лагранжа представляют в виде линейной комбинации многочленов степени n:

 Скачать реферат