Численные методы
Из рисунка очень легко получить итерационную формулу метода, используя геометрический смысл производной. Если f(x) имеет непрерывную производную f’(x)≠0, тогда получим
![]()
![]()
Аналогично получаем x2, x3, и т.д. Таким образом, можем записать общую формул
у:
![]()
Метод Ньютона можно рассматривать, как частный случай метода простых итераций, если задать
![]() .
.
В этом случае
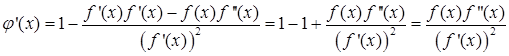
Условие сходимости метода простых итераций можно переписать для метода Ньютона следующим образом:
![]()
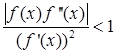
![]() (14)
(14)
Рассуждения по поводу выбора начального приближения в методе Ньютона такие же, как и в методе простых итераций, только вместо (11) используется (14). Для данного метода также применимо (13). Напишем блок-схему алгоритма метода Ньютона.
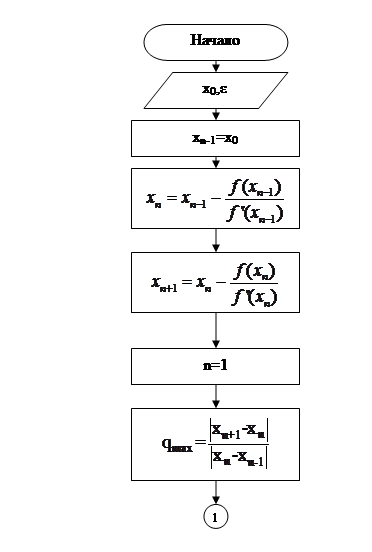

Метод секущих
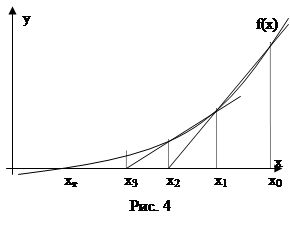
В данном методе, в отличие от метода Ньютона, проводятся не касательные, а секущие (Рис. 4). Из рисунка легко получить итерационную формулу:
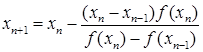 . (15)
. (15)
В качестве начального приближения необходимо задать не только x0, но и x1. Метод секущих имеет одно преимущество перед методом Ньютона – здесь не нужно вычислять производную. Но этот метод имеет также существенные недостатки. Сходимость итераций может быть немонотонной не только вдали от корня, но и в малой окрестности корня.
В знаменателе формулы (15) стоит разность значений функции. Вдали от корня это не существенно; но вблизи корня, особенно корня высокой кратности, значения функции малы и очень близки. Возникает потеря значащих цифр, приводящая к «разболтке» счёта. Это ограничивает точность, с которой можно найти корень; для простых корней это ограничение не велико, а для кратных может быть существенным.
От «разболтки» страхуются так называемым приёмом Гаврика. Выбирают не очень малое ε, ведут итерации до выполнения условия |xn+1-xn|<ε и затем продолжают расчёты до тех пор, пока |xn+1-xn| убывают. Первое же возрастание обычно означает начало «разболтки»; тогда расчёт прекращают и последнюю итерацию не используют. Все ограничения по сходимости итераций для данного метода такие же, как и в методах простых итераций и Ньютона. А вот определение достижения заданной точности, как видно из описания метода, затруднительно, и, даже, возможна ситуация, когда из-за «разболтки» счёта заданная точность не будет достигнута никогда. При использовании метода секущих в явном виде определить точность трудно, поэтому используют косвенный метод. Считают, что вблизи корня |xn+1-xn|~|xт-xn+1|. Конечно эта оценка весьма примерна, но при больших n (в идеале при n→∞) это так и есть. Построим блок-схему алгоритма данного метода с использованием приёма Гаврика.


Численные методы вычисления определённых интегралов
Метод левых прямоугольников
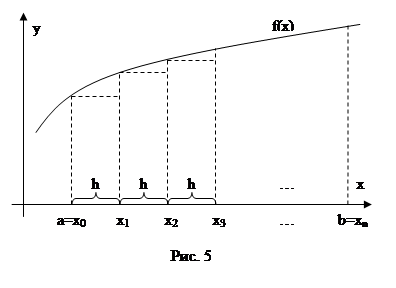
Эти методы численного интегрирования основываются на геометрическом смысле интеграла. Как известно интеграл 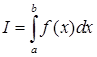 есть площадь криволинейной трапеции ограниченной подынтегральной функцией f(x) на отрезке [a,b]. Для вычисления интеграла I отрезок [a,b] разбивают на n отрезков длиной h. На каждом отрезке криволинейную трапецию приближают прямоугольником, так как его площадь можно легко вычислить. Затем суммируют все полученные площади, получая тем самым приближённое значение интеграла. На рис. 5 проиллюстрирован, так называемый, метод левых прямоугольников. Его название объясняется тем, что высота прямоугольника f(x) вычисляется в левой границе отрезка h. Выведем формулу для приближённого вычисления интеграла I.
есть площадь криволинейной трапеции ограниченной подынтегральной функцией f(x) на отрезке [a,b]. Для вычисления интеграла I отрезок [a,b] разбивают на n отрезков длиной h. На каждом отрезке криволинейную трапецию приближают прямоугольником, так как его площадь можно легко вычислить. Затем суммируют все полученные площади, получая тем самым приближённое значение интеграла. На рис. 5 проиллюстрирован, так называемый, метод левых прямоугольников. Его название объясняется тем, что высота прямоугольника f(x) вычисляется в левой границе отрезка h. Выведем формулу для приближённого вычисления интеграла I.
Как видно из рисунка площадь первого слева прямоугольника S0=f(x0)h. Площадь следующего S1=f(x1)h. Легко заметить, что площадь i-го прямоугольника Si=f(xi)h. Всего таких прямоугольников n, нумерация их ведётся от 0 до n-1. Таким образом, приближённое значение интеграла, полученное этим методом, вычисляется по формуле:
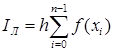 . (16)
. (16)
Оценим погрешность формулы (16) на отрезке [xi,xi+h]. Для этого разложим функцию f(x) по формуле Тейлора, выбирая xi за центр разложения и предполагая наличие у функции требуемых по ходу рассуждений непрерывных производных.
f(x)=f(xi)+(x-xi)f’(xi)+… (17)
В формуле (17) для определённости отбросим члены, содержащие производные высших порядков, т.е. 2-ю и выше. Тогда получим:
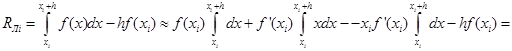
![]()
![]() , т.е.
, т.е.
![]() (18)
(18)
Чтобы получить общую погрешность метода на отрезке [a,b] просуммируем все RЛi:
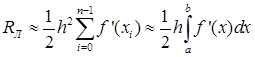 (19)
(19)
Поскольку в (17) были отброшены члены, содержащие более высокие степени длины интервала, то выражение остаточного члена (19) является асимптотическим, т.е. выполняющимся при h→0 с точностью до членов более высокого порядка малости. Но для справедливости этой оценки необходимо существование непрерывной f’(x); если f’(x) кусочно-непрерывна, то удаётся сделать лишь мажорантную оценку
![]() (20)
(20)
Эту формулу можно записать иначе
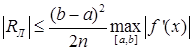 , (21)
, (21)
где n – количество отрезков, на которые разбит отрезок [a,b].
Перед началом вычислений по данному методу необходимо определиться с h или, что, по сути, то же самое, с n. Пусть известны границы отрезка [a,b], задана подынтегральная функция f(x) и точность ε, с которой должен быть вычислен интеграл. Чтобы определить h и n воспользуемся простым и очевидным неравенством:
|RЛ|≤ε, (22)
откуда получаем для непрерывной f’(x):
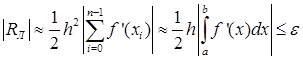
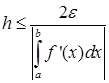 (23)
(23)
либо если учесть, что ![]() получим
получим
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
