Исследование зависимости между объемом производства, капитальными вложениями и выполнением норм выработки

ЧАСТЬ 1

Постановка задачи

Для производства двух видов продукции А и Б используются три типа ресурсов. Нормы затрат ресурсов на производство единицы продукции каждого вида, цена единицы продукции каждого вида, а также запасы ресурсов, которые могут быть использованы предприятием, приведены в табл. 2.2.

Таблица 2.2

Требуется:

I. Cформулировать экономико-математическую модель задачи в виде ОЗЛП.

II. Привести ОЗЛП к канонической форме.

III. Сформулировать экономико-математическую модель задачи двойственной к исходной.

IV. Построить многогранник решений (область допустимых решений) и найти оптимальную производственную программу путем перебора его вершин и геометрическим способом.

V. Решить задачу с помощью симплекс-таблиц.

Решение:

I. Оптимизационная модель задачи запишется следующим образом

а) целевая функция

б) ограничения: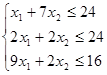

в) условия неотрицательности переменных х1≥0 ; х2≥0.

II. Приведем ОЗЛП к канонической форме. Для этого введем дополнительные переменные x3, x4 и x5.

а) целевая функция

б) ограничения: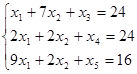

в) условия неотрицательности переменных

III. Сформулируем экономико-математическую модель задачи двойственную к исходной. Матрица В условий прямой задачи и матрица В’ – транспонированная матрица В – имеют следующий вид:

В двойственной задаче нужно найти минимум функции

Z = 24y1 + 24y2 +16y3, при ограничениях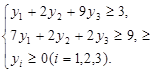

Систему ограничений-неравенств двойственной задачи обратим в систему уравнений:

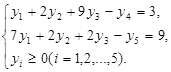
Компоненты у1, у2, у3 оптимального решения двойственной задачи оценивают добавочные переменные х3, х4, х5 прямой задачи.

1) х1+7х2≥24 (0;3,43) (24;0)

2) 2х1+2х2≥24 (0;12) (12;0)

3) 9х1+2х2≥16 (0:8) (1,78;0)

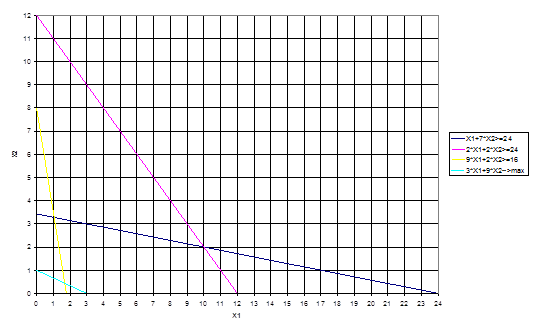
Однако нам необходимо найти такую точку, в которой достигался бы max целевой функции.

Оптимальную производственную программу можно найти двумя способами:

1) путем перебора его вершин

Находим координаты вершин многоугольника ABCDE и подставляя в целевую функцию находим ее значение.

А: А (0; 0) Z(A) =3×0+9×0=0

В: В (0; 3,43) Z(B) = 3×0+9×3,43=30,87

D: D (1,78; 0) Z(B) = 3×1,78+9×8=5,38

С: – это пересечение первого и второго уравнений

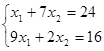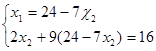;;216 -63x2+2x2=16; x2=1,04.

С (1,04; 3,28) Z(C) = 3×1,04+9×3,28=32,64

Находим max значение целевой функции. Оно находится в точке

С (1,04; 3,28). Таким образом max прибыль составит 32,68у.д.е. при выпуске продукта Р в количестве 1,04 у.е. и R – 3,28 у.е.

2) геометрическим способом

Целевая функция геометрически изображается с помощью прямой уровня, т.е. прямой на которой Z=3X1+9X2 – принимает постоянное значение.

Если С – произвольная const, то уравнение прямой имеет вид

3X1+9X2=С

При изменении const С получаем различные прямые, параллельные друг другу. При увеличении С прямая уровня перемещается в направлении наискорейшего возрастания функции Z, т.е. в направлении ее градиента. Вектор градиента

 Скачать реферат