Исследование зависимости между объемом производства, капитальными вложениями и выполнением норм выработки

или

Итак, с вероятностью 0,588 можно утверждать, что неизвестное знамение параметра регрессии содержится в интервале

<

p>При построении доверительного интервала для коэффициента корреляции генеральной совокупности прибегают к преобразованию Фишера по формуле (3.46):

Подставляя выборочный коэффициент корреляции получаем значение :

Стандартную ошибку вычисляем по приближенной формуле (3.47):

0,333.

Доверительные границы для величины на заданном уровне значимости определяются по формуле (3.48): .

При уровне значимости . Таким образом, доверительные границы для величины при будут следующими:

или

и доверительный интервал для

Доверительные границы для коэффициента корреляции находят путем обратного пересчета величины по формуле (3.49):

=

Итак, с вероятностью 0,55 можно утверждать, что коэффициент корреляции в генеральной совокупности содержится в интервале

2.

Коэффициент регрессии показывает, что объём производства в среднем возрастает на 5,5514*10000 = 55514 т/ч, если средний процент выполнения норм увеличился на 1%

Коэффициент Корреляции

Получен очень высокий коэффициент корреляции. Это свидетельствует о том, что связь между объёмом производства и средним процентом выполнения норм.

Содержание этого этапа заключается в статистической проверке значимости (надежности): уравнения регрессии, коэффициентов регрессии и корреляции.

1. Значимость уравнения регрессии определяется возможностью надежно прогнозировать среднее отклика по заданным значениям факторной переменной. Так как – случайные величины, то полученное уравнение регрессии может существенно отличаться от того «истинного» уравнения, которое соответствует генеральной совокупности.

Для оценки надёжности выборочного уравнения регрессии применяется - критерий Фишера, рассчитываемый по формуле:

(3.37)

(3.38)

где – дисперсия результативного признака, обусловленная регрессией, т.е. влиянием на факторных переменных, включенных в модель; – дисперсия результативного признака, обусловленная влиянием второстепенных факторов и случайных помех; – объём выборки; – количество факторных переменных.

Для оценки надежности выборочного уравнения регрессии воспользуемся формулой (3.37)

По статистическим таблицам распределения Фишера на -ном уровне значимости при числе степеней свободы и находим критическую точку

Так как делаем вывод о значимости полученного уравнения регрессии.

Для оценки надёжности парного коэффициента корреляции применим формулу (3.43)

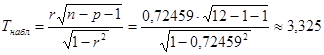
По таблице распределения Стьюдента на -ном уровне значимости при числе степеней свободы находим критическую точку

Так как делаем вывод о значимости т. е., отклоняем гипотезу об отсутствии линейной корреляционной связи в генеральной совокупности, рискуя ошибиться при этом лишь в -х случаев.

Вычислим теперь коэффициент детерминации (квадрат смешанной корреляции) Отсюда заключаем, что в случае простой регрессии общей дисперсии объём производства на 52,50 % зависит от среднего процента выполнения нормы.

Дальнейшее исследование модели связано с указанием доверительных интервалов для параметров регрессии и генерального коэффициента корреляции. Для уяснения сути этих процедур необходимы предварительные пояснения.

 Скачать реферат