Методы решения логических задач и способы их составления

ВВЕДЕНИЕ

Логические или нечисловые задачи составляют обширный класс нестандартных задач. Сюда относятся, прежде всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам. При этом часть утверждений условия задачи может выступать с различной истинностной оценкой (быть истинной или ложной). К классу логических зад

ач относятся также задачи на переливания и взвешивания.

Актуальность этой темы: Вся наша жизнь - это непрерывное решение больших и маленьких логических проблем. Без умения правильно, логически рассуждать, поступать разумно, жить трудновато.

Цели и задачи данного курса определяются той ролью, которую играет математическая логика в современных математике и информатике. В первую очередь очевидно большое значение, которое имеет математическая логика в основаниях математики. Строгое, математически точное построение логических исчислений, решение проблемы дедукции, аксиоматические системы и доказательство теорем в их рамках прививают учащимся навыки работы с математическими объектами, математическую строгость мышления, совершенно необходимую для исследовательской работы в области математики и других точных наук. В то же время быстрое развитие вычислительной техники способствует расширению как круга задач, решаемых с помощью математической логики, так и методов, применяемых для их решения. Есть люди, для которых решение логической задачи - увлекательная, но несложная задача. Их мозг как луч прожектора сразу освещает все хитроумные построения, и к правильному ответу он приходит необычайно быстро. Хотя многие культуры выработали сложные системы рассуждения, логика как эксплицитный анализ методов рассуждения получила основательное развитие изначально только в трёх традициях: в китайской, индийской и греческой. Хотя точные даты не слишком достоверны (особенно в случае Индии), скорее всего, логика возникла во всех трёх культурах в IV веке до н. э Современная логика, разработанная формально изощрённо, происходит в конечном счёте из греческой традиции (аристотелевской логики), которая, однако, была воспринята не напрямую, а при посредничестве и комментаторской деятельности арабо-мусульманских философов и средневековых европейских логиков. Можно выделить следующие исторические и региональные формы логики (приведены также их имена, исторически существовавшие и принятые в литературе по истории формальной логики):

· Древнекитайская логика

· Европейская и ближневосточная логика: традиционная логика (в широком смысле)

· Античная и раннесредневековая логика: диалектика

· Средневековая логика

· Арабская и еврейская средневековая логика

· Восточнохристианская (византийская, грузинская, армянская) средневековая логика

· Западноевропейская средневековая логика: схоластическая логика, диалектика

· Логика европейского Возрождения; диалектика

· Логика Нового времени: традиционная логика (в узком смысле), формальная логика

· Современная логика

Логика в своём развитии прошла три порога:

· порог формализации рассуждений (во всех трёх традициях)

· введение условных (символических, буквенных и числовых) обозначений (только европейская традиционная логика)

· научная революция, с которой началась современная логика, — математизация (внесение в логику математических методов).

§ 1. Решение логических задач методом графа

В течение всех лет обучения в школе мы много решаем разнообразных задач, в том числе и логических: задачи занимательного характера, головоломки, анаграммы, ребусы и т.п. Чтобы успешно решать задачи такого вида, надо уметь выделять их общие признаки, подмечать закономерности, выдвигать гипотезы, проверять их, строить цепочки рассуждений, делать выводы. Логические задачи от обычных отличаются тем, что не требуют вычислений, а решаются с помощью рассуждений. Можно сказать, что логическая задача – это особая информация, которую не только нужно обработать в соответствии с заданным условием, но и хочется это сделать. Логика помогает усваивать знания осознанно, с пониманием, т.е. не формально; создаёт возможность лучшего взаимопонимания.

Логика – это искусство рассуждать, умение делать правильные выводы. Это не всегда легко, потому что очень часто необходимая информация "замаскирована", представлена неявно, и надо уметь её извлечь. Как известно, видение рождает мышление. Возникает проблема: как установить логические связи между разрозненными фактами и как оформить в виде единой целой. Видеть ход доказательства и решения задач позволяет метод граф - схем, который делает доказательство более наглядным и позволяет кратко и точно изложить доказательства теорем и решения задач.

Задача 1. Красный, синий, желтый и зеленый карандаши лежат в четырех коробках по одному. Цвет карандаша отличается от цвета коробки. Известно, что зеленый карандаш лежит в синей коробке, а красный не лежит в желтой. В какой коробке лежит каждый карандаш?

Решение.Обозначим точками карандаши и коробки. Сплошная линия будет обозначать, что карандаш лежит в соответствующей коробке, а пунктирная, что не лежит. Тогда с учетом задачи имеем G1 (рис. 1).

Рис.1

Далее достраиваем граф по следующему правилу: поскольку в короб может лежать ровно один карандаш, то из каждой точки должны выходить одна сплошная линия и три пунктирные. Получается граф G2 , дающий решение задачи.

Задача 2. Беседуют трое друзей: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову: "Любопытно, что один из нас белокурый, другой брюнет, третий рыжий, но ни у кого цвет волос не соответствует фамилии". Какой цвет волос имеет каждый из друзей?

Решение.Построим граф отношения, заданного в условии задачи. Для этого, прежде всего, выделим множество фамилий М и множество цветов волос К, элементы которых будем обозначать точками. Точки множества М назовем буквами Б, Ч, Р (Белокуров, Чернов и Рыжов); точки второго множества – б, бр, р (белокурый, брюнет, рыжий). Если точке из одного множества соответствует точка из другого, мы их соединим сплошной линией, а если не соответствует – штриховой. Условие задачи указывает лишь на несоответствия, поэтому вначале должен возникнуть граф, изображенный на рисунке 2.

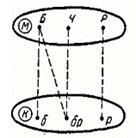
Рис.2

Из условия задачи следует, что для каждой точки из множества М существует одна и только одна точка из множеств К, которая соответствует первой и, наоборот, каждой точке из множества К соответствует одна и только одна точка из множества М. Задача сводится к тому, чтобы найти это единственно возможное соответствие между элементами множеств М и К, т. е. к нахождению трех сплошных линий, соединяющих соответствующие точки множеств.

Принцип решения задачи прост. Если какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с его третьей точкой ее необходимо соединить сплошной линией. Поэтому граф на рисунке 2 дополняется сплошными линиями, соединяющими точки Б и р, Р и бр (рис. 3).

 Скачать реферат