Статистический анализ платежного кризиса и несостоятельности российских предприятий
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тогда
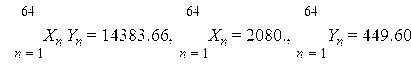
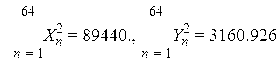
Откуда
![]()
Тогда линейная регрессия будет иметь вид
![]()
Смысл коэффициента beta заключается в том, что при изменении значения X на 1 единицу Y меняется на -0,01 единиц, т.е. каждый месяц задолженность уменьшается на 0,01 млрд.руб. Параметры показательной регрессии
![]()
![]()
![]()
Нарисуем точки и регрессию:
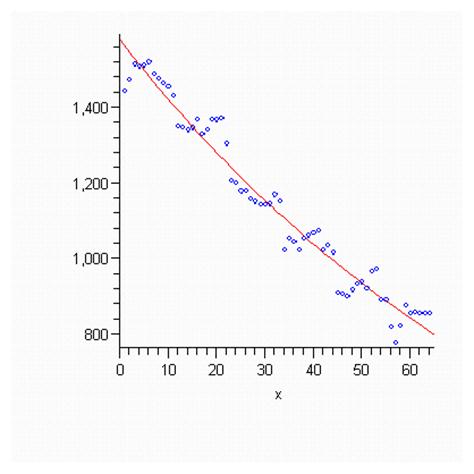
Дисперсионный анализ для линейной регрессии
Среднее Y
![]()
Остаточная вариация (RSS)
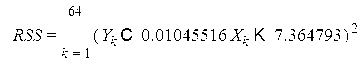
![]()
Общая вариация (TSS)
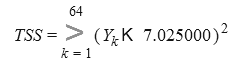
![]()
Объясняемая вариация (ESS)
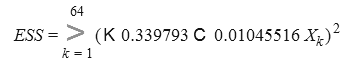
![]()
![]()
Правило сложения дисперсий выполняется
Подсчитаем оценку дисперсии ошибки, т.е. ![]()
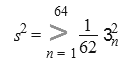
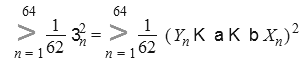
![]()
![]()
Среднее X
![]()
Найдем оценки дисперсий коэффициентов регрессии
![]()
по формулам
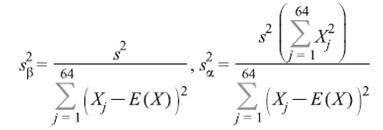
Получим
![]()
Эластичность показательной регрессии
Подсчитаем функцию эластичности по формуле
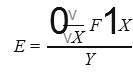
В нашем случае
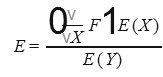
или
![]()
Значение эластичности в средней точке
![]()
Показывает, что при изменении X на 1% Y меняется на
![]()
процентов.
Изучение качества линейной регрессии
Доверительные интервалы для оцененных параметров
![]()
уровень доверия
![]()
Количество степеней свободы 62
Критическое значение статистики Стьюдента ![]()
![]()
Доверительный интервал для beta
![]()
равен
![]()
Не можем на данном уровне значимости принять гипотезу beta=0 т.к. не попадает в доверительный интервал.
Доверительный интервал для alpha
![]()
равен
![]()
Мы не можем на данном уровне значимости принять гипотезу alpha=0 т.к. не попадает в доверительный интервал.
Критерий Фишера значимости всей регрессии
Коэффициент корреляции
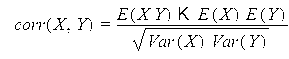
где
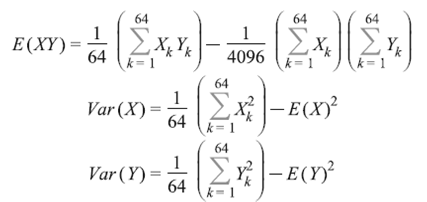
![]()
показывает, что связь сильна
Коэффициент детерминации ![]()
![]()
![]()
показывает, что регрессия объясняет 96, 03377 процентов вариации признака.
Убедимся в значимости модели с помощью статистики Фишера
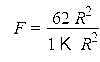
![]()
которая больше критического значения
![]()
![]()
![]()
Следовательно, регрессия значима
Проверим значимость коэффициента корреляции
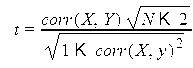
![]()
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
