Функциональные представления ограниченных дистрибутивных решеток

Пусть для произвольных . Это означает, что для каждого выполняется для подходящих , откуда 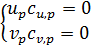для некоторых .

Домножим равенство на :

для выбранного .

Из покрытия в силу компактности спектра выберем конечное подпокрытие. Тогда , откуда получаем, что сумма идеалов совпадает с . Для некоторых получаем .

Из следует для каждого Просуммировав эти равенства, получим , или , что доказывает точность представления f.

Покажем его полноту. Пусть произвольное глобальное сечение пучка .

В силу факторности пучка сечение в каждой точке совпадает с некоторым сечением вида . По свойствам пучка эти сечения совпадают на некоторой базисной окрестности точки , а компактность простого спектра позволяет выбрать элементы так, что на и . Для любых на множестве , то есть:

: ;(1)

: ;(2)

Рассмотрим замкнутое множество . Очевидно, что .

Для каждого найдется такой , что . Тогда для каждого . Это доказывает включение: .

Действительно, , для которого .

По свойству замкнутых множеств - замкнуто и, как подмножество компактного пространства, компактно, а значит, обладает конечным покрытием.

Следовательно, в каждом из равенств (1) и (2) можно ограничиться конечным числом идеалов. Тогда:

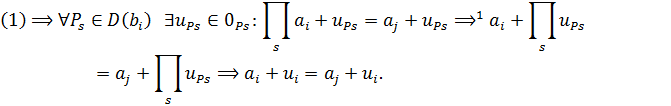
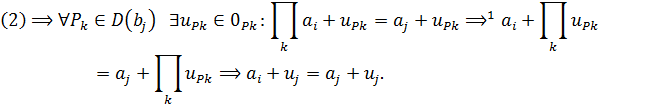
Откуда:

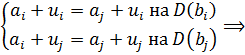
Пусть. Покажем, что :

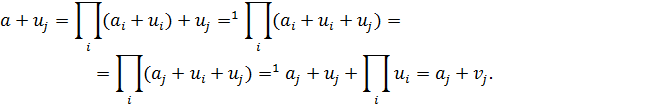
Равенство () для ограниченной дистрибутивной решетки доказывается так:

Таким образом, на для любого , и следовательно, во всех точках . Теорема доказана.

2.2 Свойства пучковых представлений

Из примера 5 видно, что для некоторых решеток функциональные пучки совпадают, для других различны. Для некоторых решеток семейства конгруэнций представлены цепями.

· Дистрибутивные решетки, для которых функциональные пучки Корниша и Ламбека совпадают

Def8. В ограниченной решетке элемент называется дополнением элемента , если и . Пусть , тогда элемент называется относительным дополнением элемента в интервале , если

Def9. Ограниченная решетка, в которой каждый элемент имеет дополнение, называется решеткой с дополнениями. Решеткой с относительными дополнениями называется решетка, в которой каждый элемент имеет относительное дополнение в любом содержащем его интервале.

В статье Е.М. Вечтомова «Аннуляторные характеризации булевых колец и булевых решеток» доказано, что для любой дистрибутивной решетки с 0: обобщенно булева решетка для каждого простого идеала в

 Скачать реферат