Функциональные представления ограниченных дистрибутивных решеток
Пусть ![]() - факторное представление решетки
- факторное представление решетки ![]() в пучке
в пучке ![]() . Для любого
. Для любого ![]() слой
слой ![]() изоморфен <
изоморфен <
img width=42 height=25 src="images/referats/7450/image184.png">, где ![]() - конгруэнция на
- конгруэнция на ![]() , «склеивающая» элементы, имеющие одинаковые образы при эпиморфизме
, «склеивающая» элементы, имеющие одинаковые образы при эпиморфизме ![]() . Зафиксируем произвольную пару
. Зафиксируем произвольную пару ![]() элементов из
элементов из ![]() .
.
Сравнимость ![]() равносильна тому факту, что глобальные сечения
равносильна тому факту, что глобальные сечения ![]() и
и ![]() совпадают в точке
совпадают в точке ![]() , следовательно
, следовательно ![]() и
и ![]() совпадают на некоторой открытой окрестности точки
совпадают на некоторой открытой окрестности точки ![]() , то есть множество
, то есть множество ![]() открыто в
открыто в ![]() .
.
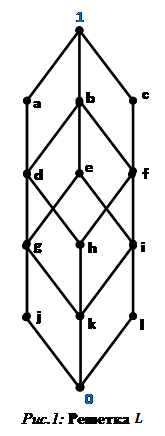
Доказательство. Если ![]() и
и ![]() – сечения, определенные над открытыми множествами
– сечения, определенные над открытыми множествами ![]() и
и ![]() , то открытым будет
, то открытым будет ![]() . Поскольку
. Поскольку ![]() открытое отображение, то
открытое отображение, то ![]() открыто, а это множество всех точек в
открыто, а это множество всех точек в ![]() , в которых совпадают
, в которых совпадают ![]() и
и ![]() .
.
Семейство конгруэнций (![]() ) на решетке
) на решетке ![]() , индексированное точками
, индексированное точками ![]() топологического пространства
топологического пространства ![]() , называется открытым семейством, если для любых
, называется открытым семейством, если для любых ![]() множество
множество ![]() открыто в
открыто в ![]() .
.
Пример 5. Функциональные пучки Ламбека и Корниша
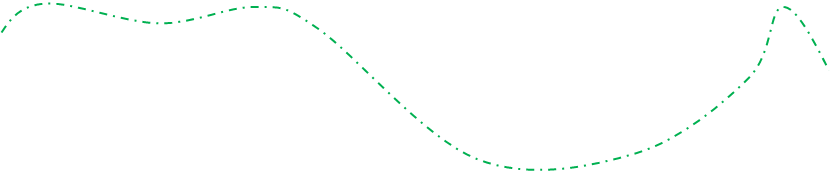
· Для решетки ![]() (Рис1) построим
(Рис1) построим ![]() (Рис.6).
(Рис.6).
|

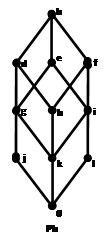

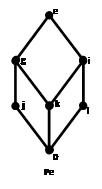
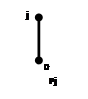
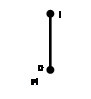
|
0Pa={a,d,g,h,j,k,0} |
0Pe={0,l,j} |
|
0Pb={0,l,j} |
0Pj={0,l,j,a,d,g,h,k} |
|
0Pc={c,f,h,I,k,l,0} |
0Pl={0,l,j,c,f,I,h,k} |
Для каждого ![]() построим фактор решетки по конгруэнциям Ламбека(Рис.7) и Корниша(Рис.8), для конгруэнций Корниша найдем 0-компоненты идеалов.
построим фактор решетки по конгруэнциям Ламбека(Рис.7) и Корниша(Рис.8), для конгруэнций Корниша найдем 0-компоненты идеалов.

|
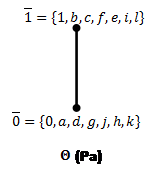
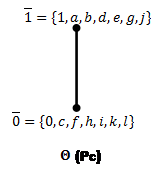
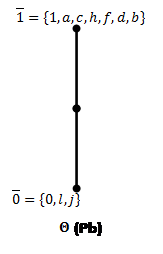
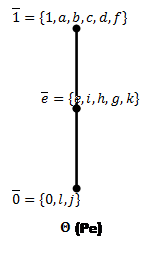
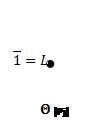
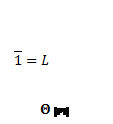
Рис.7: Решетки конгруэнций Ламбека по простым идеалам (![]() )
)
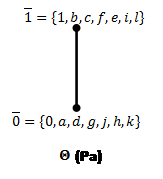
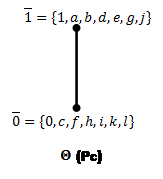
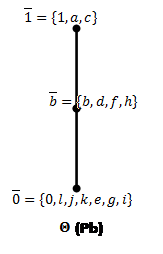
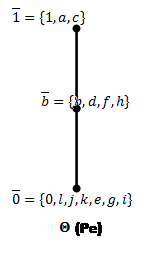

Рис.8: Решетки конгруэнций Корниша по простым идеалам (![]() ).
).
Построим пучки:
|










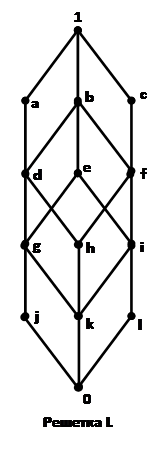
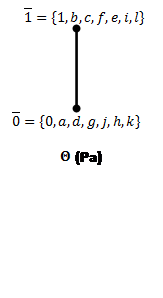
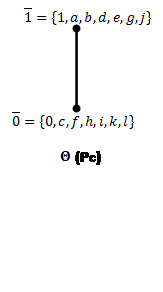
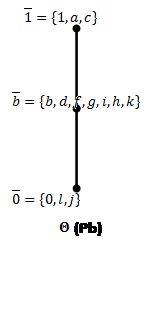
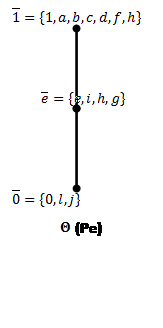
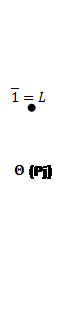
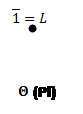

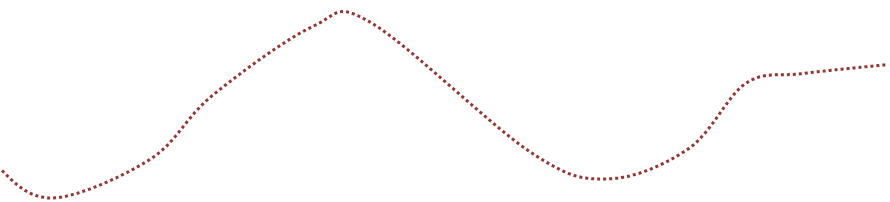
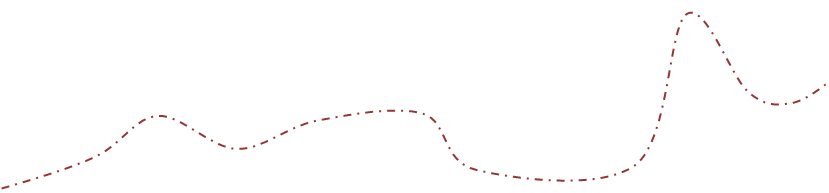
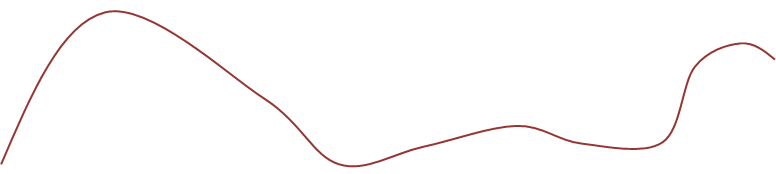

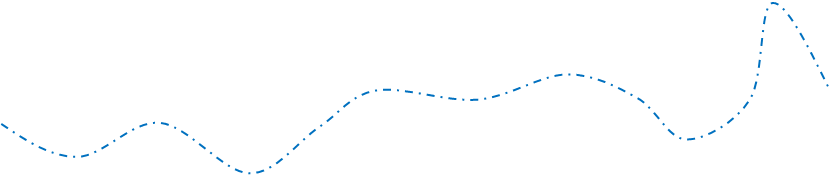






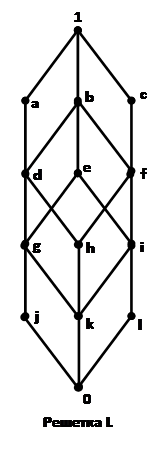
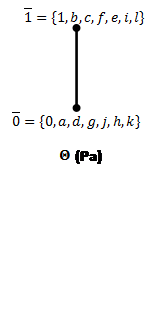
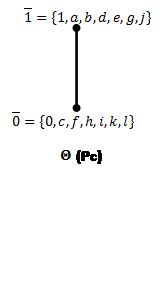
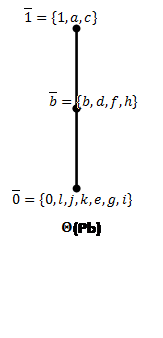
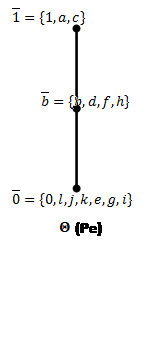
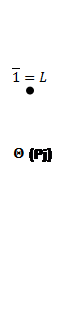
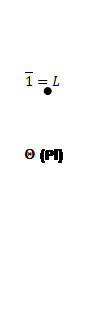
|
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
