Функциональные представления ограниченных дистрибутивных решеток

Рефераты / Математика / Функциональные представления ограниченных дистрибутивных решеток

Прибавляя к равенству получим: , что означает выполнимость .

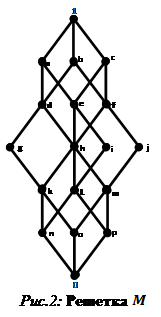
В качестве иллюстрации рассмотрим фактор-решетки rc="images/referats/7450/image101.png">и (решетка из примера 2):

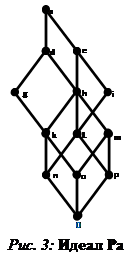
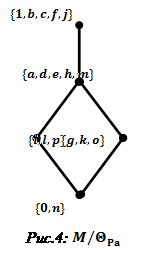
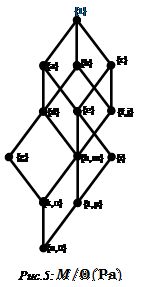
1.2 Топологическое пространство

Def4. Пусть дано множество X. Система $\mathcal{T}$ его подмножеств называется топологией на X, если выполнены следующие условия:

1. Объединение произвольного семейства множеств, принадлежащих $\mathcal{T}$ , принадлежит $\mathcal{T}$ , то есть если $U_{\alpha} \in \mathcal{T} \quad \forall \alpha \in A$ , то

$\bigcup\limits_{\alpha \in A} U_{\alpha} \in \mathcal{T}$ .

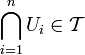2. Пересечение конечного семейства множеств, принадлежащих $\mathcal{T}$ , принадлежит $\mathcal{T}$ , то есть если $U_{i} \in \mathcal{T} \quad i = 1,\;\ldots,\;n$ , то $\bigcap\limits_{i=1}^n U_i \in \mathcal{T}$ .

3. $X,\;\varnothing \in \mathcal{T}$ .

Пара $(X,\;\mathcal{T})$ называется топологическим пространством.

Множества, принадлежащие $\mathcal{T}$ , называются открытыми множествами.

Пример 4. Обозначим через множество всех простых идеалов решетки . Для любого идеала решетки положим

и покажем, что является топологическим пространством с семейством открытых множеств вида .

Множество пусто, а . Пусть – идеалы решетки . Тогда

Таким образом, на введена топология, названная топологией Стоуна-Зарисского. Топологическое пространство с топологией Стоуна-Зарисского называется простым спектром решетки .

Иллюстрация простого спектра для решетки (Пример1, Рис.1):

Рис.6:

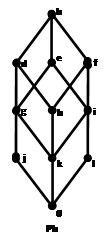
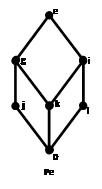
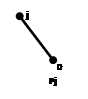
Пусть дано множество X. Семейство множеств $C = \{U_{\alpha}\}_{\alpha \in A}$ называется покрытием X, если $X \subset \bigcup\limits_{\alpha \in A} U_{\alpha}.$

Если C — покрытие множества X, то любое подмножество $D \subset C$ , также являющееся покрытием X, называется подпокрытием.

Компактное пространство — это топологическое пространство, в любом покрытии которого открытыми множествами найдётся конечное подпокрытие.

компактное пространство с базисом открытых множеств .

Доказательство Пусть для произвольного семейства идеалов . Тогда и идеал не лежит ни в одном идеале из . Это возможно лишь в случае, когда . Получим, что , значит, , для некоторых , , из семейства . Поскольку идеал содержит 1, то , что означает компактность простого спектра.