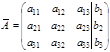Элементы линейной алгебры
Метод преобразований нахождения ранга матрицы заключается в том, что матрицу приводят к ступенчатому виду с помощью элементарных преобразований строк; количество ненулевых строк полученной ступенчатой матрицы есть искомый ранг данной матрицы.
Определение 30. Всякий отличный от нуля минор матрицы, порядок которого равен рангу матрицы, называется базисным минором этой матрицы.
Исследовани
е систем линейных уравнений.
Определение 31. Расширенной матрицей системы называется матрица системы, дополненная столбцом свободных членов. Такая матрица обозначается как ![]() .
.
Пусть дана система из m линейных алгебраических уравнений с п неизвестными.
Теорема 5. (Кронекера – Капелли решения систем уравнений). Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы:
![]() .
.
Теорема 6. Если ранг матрицы совместной системы ![]() равен числу неизвестных этой системы, то система имеет единственное решение.
равен числу неизвестных этой системы, то система имеет единственное решение.
Теорема 7. Если ранг матрицы совместной системы ![]() меньше числа неизвестных этой системы, то система имеет бесчисленное множество решений.
меньше числа неизвестных этой системы, то система имеет бесчисленное множество решений.
Для исследования однородной системы линейных уравнений пользуются следующими теоремами:
Теорема 8. Однородная система уравнений всегда совместна.
Теорема 9. Если ранг матрицы ![]() равен числу неизвестных п, то xi = 0 – единственное решение.
равен числу неизвестных п, то xi = 0 – единственное решение.
Теорема 10. Если ранг матрицы ![]() меньше числа неизвестных системы п, то система имеет множество решений.
меньше числа неизвестных системы п, то система имеет множество решений.
Правило решения произвольной системы линейных уравнений.
Найти ранг основной и расширенной матриц системы. Если ![]() , то система несовместна.
, то система несовместна.
Если ![]() , то система совместна. Тогда надо найти какой – либо базисный минор порядка r. Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить).
, то система совместна. Тогда надо найти какой – либо базисный минор порядка r. Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить).
Определение 32. Неизвестные, коэффициенты которых входят в базисный минор, называются главными, а остальные (n – r) неизвестные называются свободными.
Главные неизвестные оставляют слева, а свободные неизвестные переносят в правую часть уравнений.
По правилу Крамера найти выражения главных неизвестных через свободные неизвестные и получить общее решение системы.
Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных.
Таким образом, можно найти частные решения исходной системы уравнений.
Сводная таблица для исследования систем линейных уравнений
|
Тип системы уравнений |
Исследование системы уравнений |
Решения системы уравнений |
|
1) Однородная система с п неизвестными с п уравнениями. Например,
|
Находим значение основного определителя ∆ системы. |
|
|
Если ∆ ¹ 0, то система имеет единственное решение. |
х = у = z = 0, т. е. тривиальное решение. | |
|
Если ∆ = 0, то система имеет множество решений. |
– найти базисный минор порядка r (приведя матрицу к ступенчатому виду). Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). – по правилу Крамера найти выражения главных неизвестных через свободные неизвестные и получить общее решение системы. – придавая свободным неизвестным произвольные значения, получить соответствующие значения главных неизвестных. | |
|
2) Произвольная неоднородная система уравнений. Например,
|
Находим ранги основной и расширенной матриц. |
|
|
|
Нет решений. | |
|
|
Решить систему можно с помощью обратной матрицы или по формулам Крамера | |
|
|
Смотри решение для однородной системы уравнений при ∆ = 0. |
Решение практических задач по теме: "Линейные действия над матрицами"
Пример 8. Найти линейную операцию А + В, если
![]() ,
, ![]() .
.
Решение. Чтобы выполнить линейную операцию сложения над матрицами необходимо сложить одноименные элементы этих матриц, т. е.
![]()
Пример 9. Найти линейную операцию А − В, если
![]() и
и ![]()
Решение. Чтобы выполнить линейную операцию вычитания над матрицами необходимо вычесть одноименные элементы этих матриц, т. е.
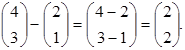
Пример 10. Найти линейную операцию 5×А, если
![]() .
.
Решение. Чтобы умножить матрицу на число необходимо помножить все элементы матрицы на это число, т. е.
![]()
Пример 11. Выполнить операцию умножения матриц, если
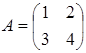 и
и 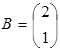 .
.
Решение. Перемножим матрицы А и В как это сделано в примере 2, т. е. элементы каждой строки первой матрицы умножаем на соответствующие элементы столбца второй матрицы.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах

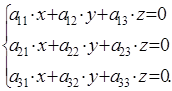
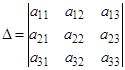
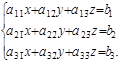
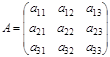 и
и