Базисные сплайны

(4)

Где

Действительно, преобразуя это выражение при получаем

Это доказывает, что всякий сплайнможет быть представлен в виде линейной комбинации функций (3), т. е. эти функции образуют базис в и представление (4) единственно. Эта формула называется представлением сплайна в виде суммы усеченных степенных функций. Итак, множествоявляется конечномерным пространством размерности

§2. Базисные сплайны с конечными носителями

В математическом анализе встречаются конструкции, связанные с финитными функциями, т. е. гладкими функциями, которые определяются на всей действительной оси, но отличны от нуля лишь на некотором конечном интервале (носителе). Ниже мы исследуем финитные сплайны из пространства . В последующем изложении они играют исключительно важную роль.

Расширим сетку , добавив дополнительно точки (можно положить, например, ).

Возьмем функциюи построим для нее разделенные разности порядка по значениям аргумента . В результате получаются функции переменной х:

Так как для разделенной разности порядка от функции по точкамсправедливо равенство

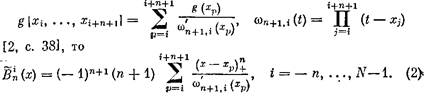
Если использовать тождество то можно получить несколько иную форму записи этой функции

Из определения усеченных степенных функций следует, что функцияявляется сплайном степени п дефекта 1 на

сетке узлов

Лемма 1.1. Справедливо тождество

Доказательство. Еслито разделенная разность функции по точкам может быть вычислена по формуле Лейбница:

Для разности порядка путем рассуждений по индукции нетрудно получить

Представим функциюв виде

и построим ее разделенную разность порядка по формуле Лейбница. Получим

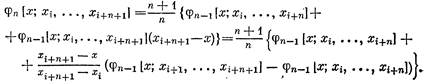
Отсюда, если учесть определение сплайнов, следует тождество (4).

Лемма 1.2. Сплайны обладают следующими свойствами:

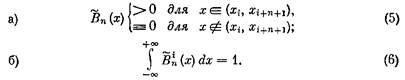
Доказательство. Функцияравна нулю при и является многочленом степени n от х при . Поэтому ее разделенные разности порядка по значениям аргументатождественно равны нулю при и т.е. Внутри интервала

В самом деле, при n = 0 согласно (2) . Пусть, далее, утверждение а) верно при Тогда при n=l в силу (4) на интервале функцияявляется линейной комбинацией с положительными весами функцийпричем по предположению в произвольной точке указанного интервала хотя бы одна из этих функций больше нуля. Следовательно, для , и утверждение а) установлено.

 Скачать реферат