Базисные сплайны

Докажем утверждение б). Всякую n+1 раз непрерывно дифференцируемую функцию g(t) на промежутке а ≤ t ≤ b можно представить формулой Тейлора с остаточным членом в интегральной форме:

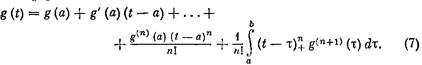
Здесь под знаком интеграла вместо обычного сомножителя стоит усеченная степенная функция, что позволяет заменить переменный верхний предел t постоянной величиной b. Из (7) следует разностное соотношение

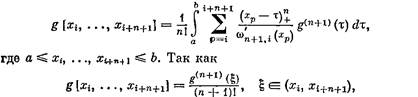
то, полагая g(x) = xn+1, поручаем

Поскольку вне интервала (а, b), то это равенство -совпадает с (6) и лемма доказана.

Лемма 1.3. Функцииявляются сплайнами степени п дефекта 1 с конечными носителями минимальной длины.

Доказательство. Предположим, что существует сплайн отличный от нуля на интервале, меньшем, чем Такой интервал, очевидно, не может иметь границей точку, не являющуюся узлом сетки . Поэтому пусть это будет интервал (xi , xi+n).

Возьмем представление сплайна дефекта v = 1 через усеченные степенные функции (1.4). Вследствие того, что при в этом представлении. Так как при то ее производные до порядка n — 1 равны нулю в точке xi+n. Имеем

Последние равенства представляют собой однородную систему линейных уравнений для определения коэффициентов . Ее определитель пропорционален определителю Вандермонда n-ro порядка, который отличен от нуля, и система имеет только нулевое решение. Наконец, из того же условия следует, что . Значит, и лемма доказана.

Теорема 1.2. Функции линейно независимы и образуют базис в пространстве сплайнов

Доказательство. Покажем сначала линейную независимость функцийна всей действительной оси. Предположим противное, т. е. что существуют такие постоянные , не все равные нулю, что

Выбирая получаем, чтои, значит, . Беря затем находим, что и т.д., т.е. Следовательно, функции линейно независимы на

Предположим теперь, что соотношение (8) выполняется только на [а, b]. Это значит, что на отрезках обращаются в нули сплайны вида

Каждый из них отличен от нуля самое большее на интервале Поэтому из предположения при xсогласно доказательству леммы 3 следует, что 0 на интервалах , а значит, и на всей действительной оси. В силу линейной независимости функций надолжно быть и это для всех i = 0, ,N-1.

Таким образом, функциилинейно независимы, и так как согласно теореме 1.1 размерность пространстваравна n+N, то они образуют базис в этом пространстве. Теорема доказана.

Функции называются базисными сплайнами с конечными носителями минимальной длины (В-сплайнами). В силу теоремы 1.2 всякий сплайн может быть единственным образом записан

 Скачать реферат