Некоторые вопросы геометрии Лобачевского на модели Пуанкаре

5. Инвариантные прямые и окружности

Из теоремы 2 следует, что прямые, проходящие через центр инверсии, и только они, отображаются при на себя, т.е. эти прямые инвариантны при .

Мы уже отмечали, что ( (O,r)) = (O,r), т.е. окружность (O,r) инвариантна при .

Существуют ли другие окружности, инвариантные при ? Ответ на этот вопрос даёт следующая.

Теорема 4. Пусть S-окружность, отличная от (O,r). (S) =S тогда и только тогда, когда S ортогональна (O,r),

Доказательство. Допустим, что (S) =S. Ясно, что S пересекает (O,r) в двух точках, скажем, A и B.

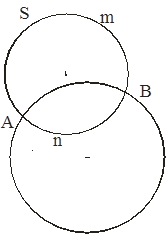
Имеем .

Согласно теореме 3

( (O,r) ^) = ( (O,r) ^),

а это означает ортогональность S и (O,r).

Докажем обратное. Пусть теперь (O,r) ортогональна S, A и B - точки пересечения S и (O,r).

Проведём в точке А касательные к S и (O,r), которые пройдут через центры окружностей (O,r) и S соответственно.

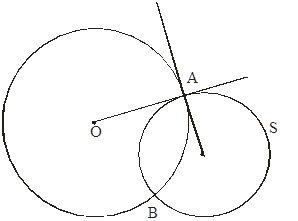
Отсюда ясно, что S-единственная окружность, ортогональная (O,r) и проходящая через точки A и B.

Так как (если допустить, что , то (S) - прямая, ортогональная (O,r) и не проходящая через точку O, что невозможно), то (S) - окружность, ортогональная (O,r) и проходящая через точки A и B. Значит, (S) =S.

Теорема 5. Окружность, проходящая через две инверсные точки, преобразуются при инверсии в себя.

Доказательство. Пусть A'=(A), S - окружность такая, что и . Пусть B - произвольная точка S и B'=, тогда

,

т.е. (B) =B', а это значит, что

(S) =S'.

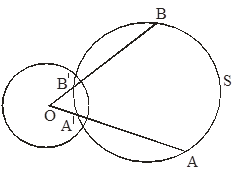
Следствие. Окружность, проходящая через две инверсные точки, ортогональна к окружности инверсии.

Рассмотрим далее две задачи, которые нам потребуются в дальнейшем изложении.

Задача 1. Дана прямая и окружность. Найти инверсию, переводящую прямую в окружность.

Дана прямая l и окружность S с центром в точке С. Проведём (СР)

l,.

Примем О за центр инверсии, тогда Р и Р' - инверсные точки, значит

r=.

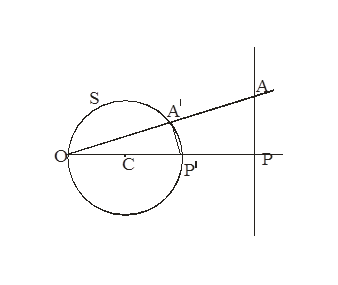
Итак,

-

искомая инверсия, переводящая прямую в окружность.

Задача 2. Даны две окружности () и (). Найти инверсию, переводящую одну окружность в другую.

Имеет место

Теорема. Любые две неравные окружности гомотетичны и имеют внутренний и внешний центр гомотетии.

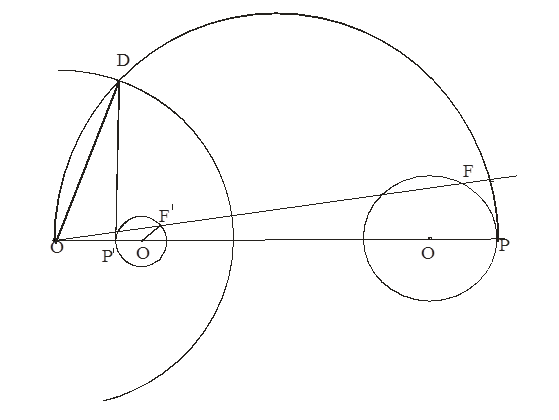
Т.к. инверсные точки, по определению, принадлежат одному лучу с вершиной в центре инверсии, то за центр инверсии выберем внешний центр гомотетии.

Пусть это точка О, тогда радиус инверсии

r=(см. рисунок).

6. Модель Пуанкаре геометрии Лобачевского на плоскости

Рассмотрим евклидову плоскость и евклидову прямую f в ней. Прямая f разбивает евклидову плоскость на две полуплоскости. Выберем одну из этих полуплоскостей без её границы и назовём плоскостью Лобачевского.

Точкой Лобачевского (Л-точкой) назовём евклидову точку, принадлежащую выбранной полуплоскости без границы f.

Прямыми Лобачевского (Л - прямыми) назовём евклидовы полуокружности (в том числе и „полуокружности бесконечно большого радиуса”, ортогональные f и расположены в выбранной полуплоскости без границы.

Определим далее отношения „лежать между", „лежать на", „быть конгруэнтными" и покажем, что при этом выполняются все аксиомы геометрии Лобачевского.

Будем говорить, что Л - точка лежит на Л - прямой, если евклидова точка лежит на евклидовой полуокружности или евклидовом луче.

Проверим выполнимость аксиом принадлежности.

Пусть даны Л - точки А и В. Покажем, что существует Л - прямая, проходящая через эти Л - точки.

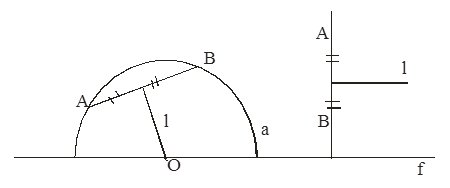
Проведём евклидову отрезку АВ срединный перпендикуляр в евклидовом смысле.

Если то евклидова полуокружность (О, |OA|) - есть

Л - прямая, если то Л - прямой будет евклидов луч.

Из указанных построений следует выполнимость и аксиомы

Каковы бы ни были точки А и В существует не более одной прямой, проходящей через эти две точки.

На каждой прямой лежат по крайне мере две точки. Существуют три точки, не лежащие на одной прямой.

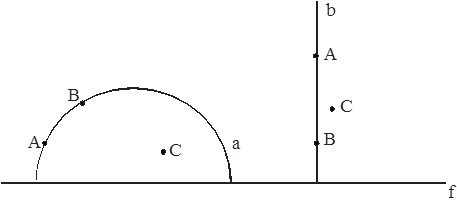
Аксиома выполняется на модели, т.к это утверждение справедливо для евклидовой полуокружности и евклидова луча.

Замечание. На следующем рисунке представлена на модели

Теорема. Две прямые имеют не более одной общей точки.

 Скачать реферат