Некоторые вопросы геометрии Лобачевского на модели Пуанкаре

Т.к. для евклидовой прямой аксиома Дедекинда справедлива, то в одном из классов или существует граничная точка .

Тогда соответствующая ей точка будет граничной в разбиении Л-прямой а.

Проверим выполнимость аксиомы Лобачевского на модели Пуанкаре.

V. Пусть дана Л-прямая а и Л-точка А, не принадлежащая а.

Покажем, что через точку А проходит, по крайне мере, две Л-прямые, не пересекающие а.

1 случай

2 случай

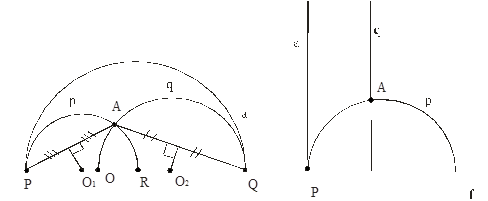
Построим евклидову полуокружность, ортогональную f и проходящую через точки P и A. Л-прямая p проходит через точку А и не пересекает а.

Аналогично строим Л-прямую q, проходящую через точку А и не пересекающую а.

Итак, существуют две Л-прямые p и q, проходящие через Л-точку А и не пересекающие Л-прямую а.

Замечание. Очевидно, что любая евклидова полуокружность, ортогональная f и проходящая через точку А и любую точку евклидова отрезка QR, не пересекает а. Таким образом, существует бесчисленное множество Л-прямых, проходящих через точку А и не пересекающих Л-прямую а.

Итак, доказана непротиворечивость геометрии Лобачевского.

В следующем параграфе покажем осуществление некоторых вопросов геометрии Лобачевского на модели Пуанкаре, где также используется инверсия.

Глава 2. Непротиворечивость геометрии Лобачевского

1. Система аксиом геометрии Лобачевского

Схема аксиоматического построения геометрии выглядит следующим образом.

1. Рассматривается множество элементов произвольной природы, которые как-то условно называют и обозначают. Далее также условно обозначают операции и отношения между элементами этого множества.

2. Даётся список аксиом, выражающих свойства основных отношений или операций.

3. Даются определения остальных понятий и путём логических рассуждений выводятся теоремы.

Система аксиом геометрии Лобачевского включает в себя: восемь аксиом связи, четыре аксиомы порядка, пять аксиом конгруэнтности, аксиому непрерывности и аксиому Лобачевского.

Основные объекты: точка, прямая, плоскость.

Основные отношения: „принадлежать", „лежать между", „быть конгруэнтными”.

Аксиомы связи

. Каковы бы ни были две точки, существует прямая, проходящая через эти две точки.

. Каковы бы ни были две точки, существует не более одной прямой, проходящей через эти две точки.

. На каждой прямой лежат две точки. Существуют три точки, не лежащие на одной прямой.

. Каковы бы ни были три точки, существует плоскость, их содержащая. На каждой плоскости есть хотя бы одна точка.

. Для любых трёх точек, не лежащих на одной прямой, существует не более одной плоскости, содержащей эти три точки.

. Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.

. Если две плоскости имеют общую точку, то существует, по крайне мере, ещё одна общая точка.

. Существуют, по крайне мере, четыре точки, не лежащие в одной плоскости.

Аксиомы порядка

. Если имеет место ABC (точка В лежит между точками А и С), то А, В, С - три различные точки, лежащие на одной прямой, и имеет место СBA.

. Для любых двух точек А и В существует, по крайне мере, одна точка С такая, что имеет место АВС.

. Из любых трёх точек, лежащих на прямой, одна и только одна лежит между двумя другими.

. (Аксиома Паша). Пусть даны три точки А, В, С, не лежащие на одной прямой, и прямая а, не проходящая ни через одну из этих точек. Если на прямой а есть точка, лежащая между точками А и В, то на прямой а есть точка, лежащая либо между В и С, либо между А и С.

Определение. Отрезком АВ назовём множество всех точек С, лежащих между А и В, и сами эти точки.

Обозначение. [AB] - отрезок АВ.

Определение. Лучом ОА назовём множество всех точек Х, что имеет место .

Обозначение. [ОА) - луч ОА.

Аксиомы конгруэнтности

. Дан отрезок UV и луч Аа. Тогда существует точка В[Aa) такая, что [AB] [UV] и [AB] [BA].

. Если [AB] [UV], [CD] [UV], то [AB] [CD].

. Если имеет место АВС и и [AB] [],

[BC] [], то [AC] [].

16

Определение. Углом назовём совокупность двух лучей с общим началом.

Определение. Треугольником АВС назовём совокупность отрезков АВ, ВС, СА.

. Дан угол (u,v) и луч Аа с заданной полуплоскостью, тогда в указанной полуплоскости существует единственный луч [Ab) такой, что (а,b) (u,v) и всякий угол конгруэнтен самому себе.

. Пусть дан АВС и, [AB] [AB], [AC] [AC], . Тогда.

 Скачать реферат