Операторные уравнения

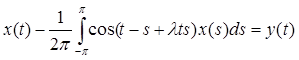Рефераты / Математика / Операторные уравнения

(1)

Это уравнение вида А()х = у() – операторное уравнение в С[-π; π], где

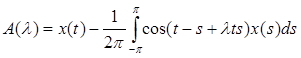
Покажем, что А(h=15 height=19 src="images/referats/3109/image063.png">) аналитична в т. 0, т.е. разлагается в ряд вида . Разложим функцию А() в ряд Тейлора: .

Найдем к– ую производную:

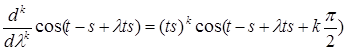
Разложим функцию в ряд Тейлора в т. 0:

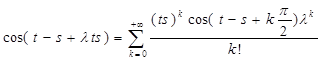
Таким образом, функция аналитична, следовательно, непрерывна при = 0, а значит, уравнение имеет единственное решение.

Операторные коэффициенты имеют вид:

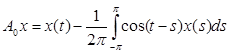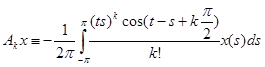; (2)

I. Начнем с уравнения А0x0 = y системы (4) §7, где у нас теперь y0=y, yк=0, к ≥ 1.

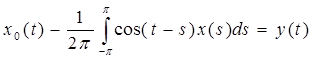
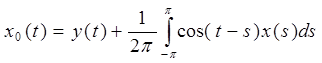
Заменим, , поэтому

, (4)

где

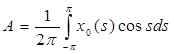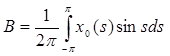
Для того, чтобы найти коэффициент А в уравнении (4), умножим его на cos t и, интегрируем по t от –π до π:

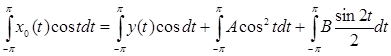подсчитаем интегралы:

, ,

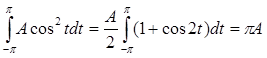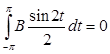
Тогда, подставив в уравнение, получаем: . Отсюда:

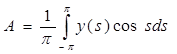. (5)

Найдем коэффициент В уравнения (4), умножив это уравнение на sin t и интегрируя по t от –π до π:

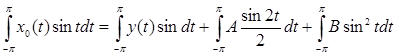Подсчитав соответствующие интегралы:

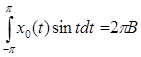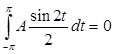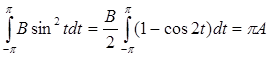, , , подставив и выразив В, получаем:

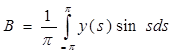. (6)

Подставим найденные коэффициенты (5) и (6) в уравнение (4):

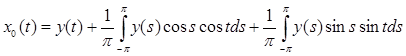
и свернем по формуле:

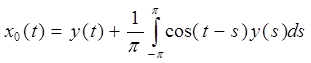
II. Найдем теперь x1(t), для этого необходимо решить следующее уравнение системы (4) §7: А0x1+А1x0 = y1. Так как y1=0 в нашем случае, то мы будем решать уравнение А0x1= – А1x0.

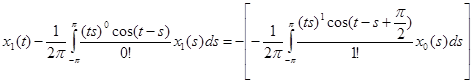
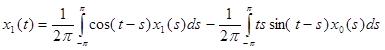
Обозначим 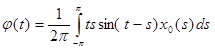, т.к. мы знаем теперь x0(s), следовательно φ(t) можно вычислить. Имеем:

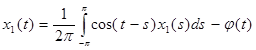
Как в предыдущем случае заменим, , поэтому

. (7)

где , .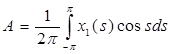

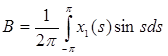Умножим уравнение (7) на cos t и проинтегрируем по t от –π до π – получим коэффициент А:

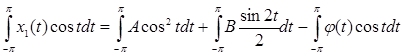
Подсчитав: , , ,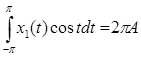

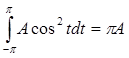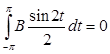имеем .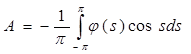

Аналогично умножив уравнение (7) на sin t и проинтегрируем по t от –π до π – получим коэффициент В: .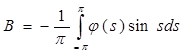

Составляем функцию x1(t), подставив коэффициенты А и В в уравнение и свернув равенство по формуле косинуса разности:

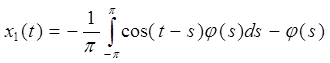Таким способом мы можем найти все остальные решения уравнения с любой степенью точности.

Пример 2. Применим метод продолжения по параметру для оценки разрешимости краевой задачи для дифференциального уравнения, а потом решим ее методом малого параметра.

–x'' + b(t)x' +c(t)x = y(t), 0< t <1, (1)

x(0) = x(1) = 0 (2)

Здесь c(t) непрерывна на [0, 1], b(t) непрерывно дифференцируема на [0, 1]. Предположим еще, что на [0, 1] c(t) – b(t)'/2 ≥ α > –8/π (*).

Покажем методом продолжения по параметру, что в этих условиях при всякой правой части y ÎY = С [0, 1] существует единственное решение задачи x Î X = С2 [0, 1] – пространству, состоящему из дважды непрерывно дифференцируемых на [0, 1] функций x(t), удовлетворяющих граничным условиям (2), и с нормой , где .