Операторные уравнения

. (3)

Отсюда видно, что в круге (2) решение является аналитической функцией параметра и,следовательно, может быть найдено в виде

(4)

На этой идее основывается метод малого параметра д

ля уравнения (1). Подставим ряд (4) в уравнение (1) и, согласно теореме единственности разложения в степенной ряд, приравниваем коэффициенты при одинаковых степенях в правой и левой частях получившегося тождества:

.

Таким образом, мы приходим к следующей рекуррентной системе уравнений для определения x0, x1, …:

Аx0=y, Аx1=Сx0, …, Аxк=Сxк-1, …

Так как А непрерывно обратим, то отсюда последовательно находим

x0=А–1y, x1= А–1(СА–1)y, …, xк= А–1(СА–1)кy, …

Следовательно,

. (5)

Мы получили решение (3), разложенное в степенной ряд. Если мы хотим оборвать степенной ряд и ограничиться приближенным решением

то можно оценить ошибку. Вычитая из ряда (5) его частичную сумму (6) и оценивая разность по норме, получим

.

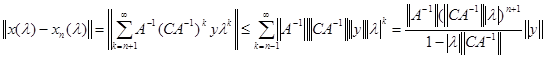§7. Метод малого параметра в общем случае

Пусть дано уравнение

А()х = у(). (1)

Здесь А()ÎL(X,Y) задана при каждом , , или, как говорят, А() – оператор-функция. Пусть А() аналитична при =0, а оператор А(0) непрерывно обратим, у() – заданная аналитическая функция при =0 со значениями в Y. Неизвестное x разыскивается в X.

Аналитичность А() и у() в точке 0 означает, что они разлагаются в следующие степенные ряды с ненулевыми радиусами сходимости, которые равны и соответственно:

, . (2)

Из аналитичности А() следует непрерывность А() при =0. следовательно, найдется число r > 0 такое, что в круге

.

Отсюда вытекает, что в круге оператор-функцияА() непрерывно обратима и, следовательно, уравнение (1) имеет единственное решение

,

при этом x() аналитична в точке =0 и радиус сходимости соответствующего степенного ряда равен min(, r). Для фактического построения x() удобно воспользоваться методом малого параметра. Будем разыскивать x() в виде

. (3)

Подставляя ряд (3) в уравнение (1) и учитывая разложения (2), приходим к следующей системе для неопределенных коэффициентов x0, x1, x2, …:

А0x0 = y0, А0x1+А1x0 = y1,

А0x2 + А1x1 + А2x0 = y2, (4)

. . . . . . . . . . .

, …

Здесь А0 = А(0) непрерывно обратим. Решая последовательно уравнения получившейся системы, находим

, , … (5)

Возникающие здесь формулы довольно громоздки, однако этим путем можно найти решение уравнения с любой степенью точности. Метод малого параметра особенно удобен в тех случаях, когда обращение оператора А(0) – задача более простая, чем задача обращения оператора А().

§8. Метод продолжения по параметру

8.1. Формулировка основной теоремы

В качестве еще одного приложения теорем об обратных операторах рассмотрим один из вариантов метода продолжения по параметру. Пусть и А непрерывно обратим. Если , то, согласно теореме 9 §3, В также непрерывно обратим. Оказывается, при определенных условиях можно доказать, что В будет непрерывно обратим и в том случае, когда он очень далек от А. Идея заключается в следующем. Рассмотрим непрерывную на отрезке [0, 1] оператор - функцию такую, что А(0)=А, А(1)=В. Иначе говоря, в L(X, Y) рассматривается непрерывная кривая, соединяющая точки А и В. Будем предполагать, что для оператор – функции выполняется следующее условие:

1. Существует постоянная такая, что при всех и при любых справедливо неравенство

. (1)

Ниже будет доказана следующая теорема.

Теорема 14. Пусть А(λ) – непрерывная на [0, 1] оператор-функция (при каждом ), причем оператор А(0) непрерывно обратим. Если для А(λ)выполняется условие I, то А(I)непрерывно обратим, причем .

 Скачать реферат