Теория нумераций

Случай 2. Морфизм является факторизацией, а – мономорфизмом. На множестве определим отношение эквивалентности так: ="images/referats/3088/image775.png">для тогда и только тогда, когда или когда и . Рассмотрим диаграмму

где . Из определения видно, что . Тогда из того, что – факторизация, следует существование единственного морфизма такого, что . Из того, что , следует, что – мономорфизм. Проверка того, что внешний квадрат диаграммы является универсальным квадратом, аналогична случаю 1.

Случай 3. Морфизмы и являются мономорфизмами. С точностью до эквивалентности можно считать, что и морфизмы и являются просто вложениями соответственно. Положим . Из определения видно, что отображения вложения являются морфизмами из в .

Проверим, что диаграмма

является универсальным квадратом. Пусть – произвольное нумерованное множество, а :и :– такие морфизмы, что . Последнее означает в нашем случае, что ограничения и совпадают. Следовательно, существует (единственное) отображение , ограничениями которого на и являются соответственно и . Проверим, что есть морфизм из в . Действительно, пусть таковы, что . Функцию определим так:

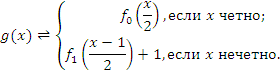
Ясно, что . Проверим, что . Действительно, . То, что и , следует из определения .

Общий случай. Пусть и – произвольные морфизмы. Построим следующую диаграмму (используя канонические представления морфизмов и ):

 Скачать реферат