Теория нумераций

Отношение , определенное на множестве H(S) всех нумераций множества S является транзитивным. Следовательно, отношение на H(S) является предпорядком.

Если и для , то эти нумерации эквивалентны и обозначаются . Класс нумераций эквивалентных нумерации обозначим через []. Множество классов эквивалентных нумераций обозначим через L(S).

На множестве H(S) можно задать операцию прямой суммы нумераций . Пусть нумерации , определим нумерацию следующим образом:

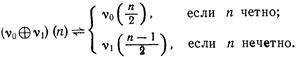
Основное свойство операции следующее:

Предложение 3

Пусть тогда сводится к тогда и только тогда когда сводится к и сводится к .

Обозначим через семейство всех вычислимых нумераций и через семейство классов эквивалентных вычислимых нумераций .

Главные нумерации

Рассмотрим понятие главной нумерации для семейства рекурсивно перечислимых множеств. Это понятие позволяет ответить (в случае семейства рекурсивно перечислимых множеств) на вопрос: «какую нумерацию данного множества следует считать наиболее естественной?»

Нумерацию назовем главной, если любая нумерация сводится к .

Нумерацию назовем минимальной, если следует что .

У семейства может существовать не более одной с точностью до эквивалентности главной нумерации. Минимальных нумераций может существовать очень много.

Предложение 1

Семейства обладают главными вычислимыми нумерациями.

Семейство назовем главным подмножеством, если оно обладает главной вычислимой нумерацией.

Предложение 2

Главное подмножество замкнуто относительно объединения возрастающих вычислимых последовательностей своих элементов.

Семейство назовем -подмножеством , если существует частично рекурсивная функция g такая что выполнены условия:

1. если то ;

2. если , то и

Предложение 3

Всякое непустое -подмножеством является главным.

Существуют естественные классы рекурсивно перечислимых множеств, которые не имеют главной вычислимой нумерации. Таковыми, например, являются любые семейства общерекурсивных функций.

Определим понятие предельной точки для семейства.

Одноместная (всюду определенная) функция h называется предельной точкой для семейства S, если для любого nN в S найдется функция g отличная от h такая что .

Предложение 4

Если вычислимое семейство содержит предельную точку, то S не имеет главной вычислимой нумерации.

Следствие

Семейство всех одноместных примитивно рекурсивных функций не имеет главной вычислимой нумерации.

Отделимые нумерации

Во многих вопросах, связанных с употреблением нумераций, важно знать, какие отношения между элементами нумерованного множества можно эффективно распознать по их номерам. Одним из самых первых вопросов является следующий: можно ли по номерам двух элементов эффективно узнать, являются ли они Равными или нет? Те нумерации, для которых этот вопрос решается положительно, называются разрешимыми.

Пусть – нумерация множества S. Рассмотрим бинарное отношение на множестве N определенное так . Отношение является отношением эквивалентности и называется нумерационной эквивалентностью. Нумерация называется разрешимой, если отношение рекурсивно. Нумерацию называется позитивной (негативной) если () рекурсивно перечислимо.

Отношение эквивалентности () на множестве S называется разрешимым (позитивным, негативным), если S рекурсивно (рекурсивно перечислимо, представляет собой дополнение до рекурсивно перечислимого множества).

 Скачать реферат