Алгоритм решения Диофантовых уравнений
Формула любого составного числа, соответствующего этой матрице, имеет вид - (![]() i + 1) (
i + 1) (![]() j + 1), где
j + 1), где ![]() i - номер столбца этой матрицы,
i - номер столбца этой матрицы,
![]() j – соответственно, номер строки этой матрицы. Для верхней строки (
j – соответственно, номер строки этой матрицы. Для верхней строки (![]() = 1) формула составного числа примет вид – 2(
= 1) формула составного числа примет вид – 2(![]() i + 1) – это ряд чётных чисел.
i + 1) – это ряд чётных чисел.
Всё это пока заготовка для доказательства великой теоремы Ферма (ВТФ).
Нечётные числа примут вид 2(![]() i + 1) ± 1. В нашем случае пусть нечётные числа будут - 2(
i + 1) ± 1. В нашем случае пусть нечётные числа будут - 2(![]() i + 1) - 1.
i + 1) - 1.
Чтобы доказать ВТФ надо рассмотреть три варианта:
- I X - чётное число, У - чётное число, Z - чётное число;
- II X - чётное число, У - нечётное число, Z - нечётное число;
- III X - нечётное число, У - чётное число, Z - нечётное число.
Вариант I. Пусть уравнение ВТФ верно для чётных чисел.
В формулу ВТФ вставим аналитические выражения чётных чисел.
[2(![]() 1 + 1)]n = [2(
1 + 1)]n = [2(![]() 2 + 1)]n + [2(
2 + 1)]n + [2(![]() 3 + 1)]n ,
3 + 1)]n ,
где для определённости возьмём ![]() 1 >
1 > ![]() 2 >
2 > ![]() 3
3
После упрощения.
(![]() 1 + 1)n = (
1 + 1)n = (![]() 2 + 1)n + (
2 + 1)n + (![]() 3 + 1)n
3 + 1)n
По сути, природа этого уравнения та же, что и уравнения ВТФ, т.к. зависимость между Х, У, Z и столбцами матрицы ![]() i – функции соответствующие линейным уравнениям.
i – функции соответствующие линейным уравнениям.
Можно составить систему подобных уравнений.
![]()
![]()
![]()
………………………………………… (а)
![]()
![]()
Каждое уравнение этой системы также является функциональным уравнением ВТФ.
Для обоснования данного утверждения рассмотрим следующий пример.
Вычислим несколько значений ![]() соответствующих числу 10 по формуле чётных чисел.
соответствующих числу 10 по формуле чётных чисел.
2(![]() 1 + 1)=10
1 + 1)=10 ![]() 1 =4
1 =4
2(![]() 2 + 2)=10
2 + 2)=10 ![]() 2 =3
2 =3
2(![]() 3 + 3)=10
3 + 3)=10 ![]() 3 =2
3 =2
Т.е. переменная ![]() может принимать значения от 1 до ¥.
может принимать значения от 1 до ¥.
Условием для существования системы уравнений (а) служат лишь условия
![]() и
и ![]() .
.
Данные условия слабее условий существования пифагоровых троек, где, если (а, в, с) – пифагорова тройка, то таковою будет и тройка (nа, nв, nс), при всех n = 1, 2, 3 …
Т.е. система (а) должна быть справедливой для всего ряда натуральных чисел, при условии неизменности величин р и f, и условии ![]() 3 +1<½K½<¥.
3 +1<½K½<¥.
Это следует при предположении справедливости уравнения ВТФ – ![]() .
.
У системы уравнений (а) есть 2 варианта:
- I - каждое уравнение системы имеет решение;
- II - каждое из уравнений системы не имеет решений.
Если взять в уравнении системы к = -![]() 3, тогда уравнение примет вид
3, тогда уравнение примет вид
![]()
Данное уравнение вида ![]() не может иметь решений в целых числах при n>2.
не может иметь решений в целых числах при n>2.
Тогда не верно любое уравнение системы и следовательно не верно и уравнение ВТФ.
Рассматривались чётные значения Х, У, Z.
В системе уравнений (а) переменные ![]() I принимают значения всех чисел натурального ряда, и чётных и не чётных. Тогда ВТФ тоже доказана для всего ряда натуральных чисел. Если же рассматривать варианты II и III доказательства ВТФ, тогда функциональные уравнения примут вид:
I принимают значения всех чисел натурального ряда, и чётных и не чётных. Тогда ВТФ тоже доказана для всего ряда натуральных чисел. Если же рассматривать варианты II и III доказательства ВТФ, тогда функциональные уравнения примут вид:
II [2(![]() 1+1)]n=[2(
1+1)]n=[2(![]() 2+1)-1]n+[2(
2+1)-1]n+[2(![]() 3+1)-1]n
3+1)-1]n
III [2(![]() 1+1)-1]n=[2(
1+1)-1]n=[2(![]() 2+1)]n+[2(
2+1)]n+[2(![]() 3+1)-1]n
3+1)-1]n
Принципиально в доказательстве ВТФ это ничего не меняет.
Для обоснования данного, довольно – таки экзотического на сегодняшний день метода, далее будут рассмотрены некоторые известные задачи.
Уравнение Пелля
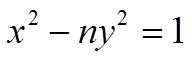 (1)
(1)
Рассмотрим 3 варианта:
- I Х - чётное число, У - нечётное число, n - нечётное число;
- II Х - нечётное число, У - нечётное число, n - чётное число;
- III Х - нечётное число, У - чётное число, n – любое, и чётное, и нечётное число.
И всегда ½Х½ > ½У½
Вариант I.
Составим функциональное уравнение.
![]() , где, конечно же,
, где, конечно же, ![]() 1 >
1 > ![]() 2
2
Возьмём к = - ![]() 2, тогда
2, тогда
![]()
После преобразований
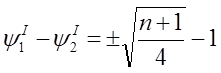 (2)
(2)
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
