Алгоритм решения Диофантовых уравнений

е) , при m=2, У=8;

Решим уравнение (X-Z)(X+Z)=64 перебором произведений

64=1х64; 2х32; 4х16.

Из соотношения 2х32, получаем

	>

т.е.

Система

Даёт значения

ж) - нет корней в целых числах.

з) , при m=2, У=12 и т.д.

Разберём до конца У=12 и соответственно У2=144.

Число 144 даёт следующие интересующие нас произведения

144=2х72; 4х36; 6х24; 8х18.

Из формулы (Х-Z)(X+Z)=У2 получим следующие значения Х, У, Z.

и) - нет корней в целых числах.

к) - нет корней в целых числах.

л) - нет корней в целых числах.

м) - нет корней в целых числах.

Рассмотрим следующий вариант:

- пусть все три числа чётные и Х>У>Z, как и > > .

Заранее знаю, что после сокращения всех членов на 22 уравнение перейдёт в область всех натуральных чисел.

Из последнего уравнения составим три системы уравнений, после соответствующих преобразований, используя соотношения

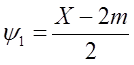
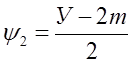
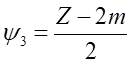
Рассмотрим все три полученные системы уравнений (н), (п), (р).

н) и преобразуя – Z=2m, получились все чётные числа при m ≥1.

В таблице приведены значения троек для m ≤10, при условии Х-У=2.

п) - то же выражение, что и в (н).

 Скачать реферат