Многочлены Лежандра, Чебышева и Лапласа
Необходимость применения численного преобразования Лапласа возникает вследствие того, что таблицы оригиналов и изображений охватывают далеко не все встречающиеся в практике случаи, а также вследствие того, что оригинал или изображение зачастую выражаются слишком сложными, неудобными для применений формулами.
Проблема обращения преобразования Лапласа, как задача отыскания решения f(x) интегр
ального уравнения первого рода (6), относится к классу некорректных задач и может быть решена, в частности, посредством регуляризирующего алгоритма.
Задачу численного обращения преобразования Лапласа можно также решать методами, основанными на разложении функции-оригинала в функциональный ряд. Сюда в первую очередь можно отнести разложение в степенной ряд, в обобщенный степенной ряд, в ряд по показательным функциям, а также в ряды по ортогональным функциям, в частности по многочленам Чебышева, Лежандра, Якоби и Лагерра. Задача разложения оригинала в ряды по многочленам Чебышева, Лежандра, Якоби в окончательном своем виде сводится к проблеме моментов на конечном промежутке. Пусть известно преобразование Лапласа F(p) функции β(t)f(t):
![]()
где f(t) - искомая функция, а β(t) - неотрицательная, интегрируемая на [0,∞) функция. Предполагается, что функция f(t) интегрируема на любом конечном отрезке [0, Т] и принадлежит классу L2(β(t), 0, ∞).По изображению F(р).функции β(t), f(t), функция f(t) строится в виде ряда по смещенным многочленам Якоби, в частности по смещенным многочленам Лежандра, Чебышева первого и второго рода, коэффициенты которого ak вычисляются по формуле.
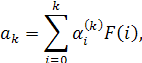
где ![]() - коэффициенты смещенного многочлена Лежандра, Чебышева первого и второго рода соответственно, записанных в виде
- коэффициенты смещенного многочлена Лежандра, Чебышева первого и второго рода соответственно, записанных в виде ![]()
Другим приемом численного обращения преобразования Лапласа является построение квадратурных формул для интеграла обращения (8).
4. Обращение преобразования Лапласа с помощью многочленов, ортогональных на конечном промежутке
4.1 Постановка задачи
Задачу преобразования Лапласа можно решать методами, основанными на разложении оригинала в ряды по ортогональным функциям, в частности по многочленам Чебышева, Лежандра и Якоби.Эта задача, которая в окончательном своем виде сводится к проблеме моментов на конечном промежутке, была подвергнута изучению в работах многих авторов.
Рассмотрим постановку этой задачи в таком виде, как это сделано в работах В.М. Амербаева и в книге В.А. Диткина и А.П. Прудникова [2].
Пусть известно преобразование Лапласа F(p) функции β(t)f(t):
![]() (10)
(10)
Где f(t) – искомая функция, а β(t) – неотрицательная, абсолютно интегрируемая на [0,∞) функция. Предположим, что функция f(t) интегрируема на любом конечном отрезке [0, Т] и принадлежит классу L2(β(t), 0, ∞):
![]() (11)
(11)
Требуется по изображению F(р) функции β(t)f(t), построить функцию f(t).
В интеграле (10) введем замену переменной x=e-t; тогда он приведется к виду
![]() (12)
(12)
где
![]()
В силу условий, которые наложены на функции f(t) и β(t), интеграл (12) сходится всюду в плоскости Re p≥,0, поэтому переменной р можно придать значения 0, 1, 2, … и получить «взвешенные моменты» функции ![]()
![]() (13)
(13)
После этого решаемую задачу можно сформулировать так: найти функцию ![]() по ее «взвешенным моментам»
по ее «взвешенным моментам» ![]() , или, что тоже самое, найти функцию f(t) по значениям изображения функции β(t)f(t) в целочисленных точках p = k (k = 0, 1, 2, …). В частном случае эту задачу можно упростить и по первым п + 1 «взвешенным моментам» искать многочлен
, или, что тоже самое, найти функцию f(t) по значениям изображения функции β(t)f(t) в целочисленных точках p = k (k = 0, 1, 2, …). В частном случае эту задачу можно упростить и по первым п + 1 «взвешенным моментам» искать многочлен ![]() , такой, чтобы его «взвешенные моменты» совпадали с заданными моментами функции
, такой, чтобы его «взвешенные моменты» совпадали с заданными моментами функции ![]() , то есть чтобы выполнялись равенства
, то есть чтобы выполнялись равенства
![]() (14)
(14)
4.2.Обращение преобразования Лапласа с помощью смещенных многочленов Лежандра
Рассмотрим частный случай весовой функции
![]() (15)
(15)
![]() или
или ![]() .
.![]()
Многочленами, ортогональными на отрезке [0,1] с весом ![]() , будут смещены многочлены Лежандра
, будут смещены многочлены Лежандра ![]()
Они задаются формулой
![]() при
при ![]()
или же формулой
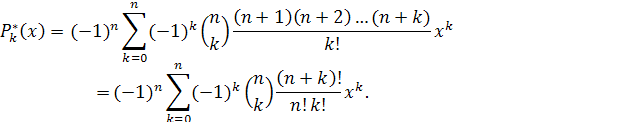
Величина rn в этом случае равна
![]()
и разложение функции f(t) по смещенным многочленам Лежандра имеет вид
![]() (16)
(16)
Величины αk вычисляются по формуле
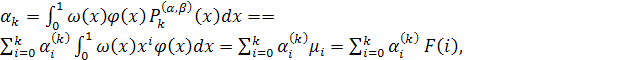 (17)
(17)
в которой ![]() - коэффициенты смещенного многочлена Лежандра
- коэффициенты смещенного многочлена Лежандра ![]()
4.3. Обращение преобразования Лапласа с помощью смещенных многочленов Чебышева первого рода.
Положим теперь ![]() Весовая функция имеет вид
Весовая функция имеет вид
![]() и
и ![]()
Смещенные многочлены Чебышева первого рода ![]() являются ортогональной системой на [0,1] по весу
являются ортогональной системой на [0,1] по весу ![]()
Многочлены Якоби ![]() отличаются от
отличаются от ![]() только численным множителем, а именно
только численным множителем, а именно
![]() ,
,
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
