Связь комбинаторики с различными разделами математики

8 перестановок типа <3, 3>,

6 перестановок типа <2, 2, 2>.

Поэтому тождественная перестановка имеет 26 неподвижных точек на М, перестановки второго и пятого типов имеют по 23 неподвижных точек на М, перестановки третьего типа – по 24, а перестановки четвёртого типа – по 22. Тогда по лемме Бернсайда получаем (26

+ 6∙23+ 3∙24+ 8∙22 + 6∙23) = 10.

Итак, число геометрически различных способов раскраски граней куба в два цвета равно 10.

Задача 4. Сколько различных ожерелий можно составить из двух синих, двух белых и двух красных бусин?

Решение. Переформулируем задачу так: сколькими геометрически различными способами можно раскрасить вершины правильного шестиугольника так, чтобы две были синего цвета, две – белого, две – красного? а) Вокруг центра шестиугольника имеется пять поворотов на углы . Им соответствуют перестановки:

1) (1, 2, 3, 4, 5, 6)

2) (1, 3, 5) (2, 4, 6)

3) (1, 4) (2, 5) (3, 6)

4) (1, 5, 3) (2, 6, 4)

5) (1, 6, 5, 4, 3, 2)

б) Имеется три симметрии относительно осей, соединяющих противоположные вершины правильного шестиугольника. Им соответствуют перестановки:

6) (1) (4) (2, 6) (3, 5)

7) (2) (5) (3, 1) (4, 6)

8) (3) (6) (2, 4) (1, 5)

в) Имеется три симметрии относительно осей, соединяющих середины противоположных сторон правильного шестиугольника. Им соответствуют перестановки:

9) (1, 2) (6, 3) (5, 4)

10) (1, 6) (2, 5) (3, 4)

11) (2, 3) (1, 4) (6, 5)

Вместе с тождественной перестановкой (1) (2) (3) (4) (5) (6) получаем 12 перестановок – все элементы группы G. Итак, в группе G имеется:

1 перестановка типа <1, 1, 1, 1, 1, 1>,

2 перестановки типа <6>,

2 перестановки типа <3, 3>,

4 перестановки типа <2, 2, 2>,

3 перестановки типа <1, 1, 2, 2>.

Определим количество неподвижных точек для перестановок каждого типа. Так как количество различных цветов, в которые нужно раскрасить шестиугольник, равно трём, то минимальное количество циклов в перестановке должно быть равно трём, чтобы она имела неподвижные точки. То есть перестановки 1), 2), 4), 5) неподвижных точек не имеют. Для перестановки первого типа получим 36 = 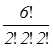= 90 неподвижных точек. Для каждой перестановки типа <2, 2, 2> по принципу умножения получаем по Р3 =3∙2∙1= 6 неподвижных точек. Для каждой перестановки типа <1, 1, 2, 2> по принципу умножения получим по Р3 =3∙2∙1∙1= 6 неподвижных точек. Применим лемму Бернсайда: (1∙90+ 4∙6+ 3∙6) = 11.

Итак, 11 различных ожерелий можно составить из двух синих, двух белых, двух красных бусин.

Задача 5. Сколькими геометрически различными способами три абсолютно одинаковые мухи могут усесться в вершинах правильного пятиугольника?

Решение. Обозначим М – множество различных способов расположения трёх одинаковых мух в вершинах пятиугольника, если вершины занумерованы. Тогда |M| = 25 (3, 2)==10 способов расположения мух, где 2 – количество элементов множества М1 = {м, с} (где м – муха, с – свободная вершина),

3, 2 – кратности соответственно м и с.

а) Вокруг центра пятиугольника имеется четыре поворота на углы . Им соответствуют перестановки:

1) (1, 2, 3, 4, 5)

2) (1, 3, 5, 2, 4)

3) (1, 4, 2, 5, 3)

4) (1, 5, 4, 3, 2)

б) Имеется пять симметрий относительно осей, соединяющих вершины пятиугольника с серединами противоположных сторон. Им соответствуют перестановки:

5) (1) (2, 5) (3, 4)

6) (2) (1, 3) (5, 4)

7) (3) (2, 4) (1, 5)

8) (4) (3, 5) (2, 1)

9) (5) (1, 4) (2, 3),

где 1, 2, 3, 4, 5 – числа, с помощью которых занумерованы вершины пятиугольника. Вместе с тождественной перестановкой (1)(2)(3)(4)(5) имеем 10 элементов группы G. Итак, в группе G имеется:

1 перестановка типа <1, 1, 1, 1, 1>,

4 перестановки типа <5>,

5 перестановок типа <1, 2, 2>.

Определим количество неподвижных точек для перестановок каждого типа. Чтобы перестановка имела неподвижные точки, минимальное количество циклов в перестановке должно быть равно двум, так как множество М1 состоит из двух элементов м и с. Поэтому перестановки 1) – 4) не имеют неподвижных точек. Тогда для перестановки типа <1, 1, 1, 1, 1> имеем по формуле: 25 (3, 2) = = 10 неподвижных точек. Для каждой перестановки типа <1, 2, 2> получим по принципу умножения по Р2 =2∙1∙1= 2 неподвижные точки. По лемме Бернсайда получаем (1∙10+ 5∙2) = 2.

Итак, двумя геометрически различными способами три одинаковые мухи могут усесться в вершинах правильного пятиугольника.

Задача 6. Сколькими способами можно раскрасить вершины куба в два цвета (красный и синий) так, чтобы вершин каждого цвета было поровну?

Решение. Для решения этой задачи воспользуемся задачей 1. Пусть М – множество всевозможных по-разному раскрашенных кубов одного размера, положение которых в пространстве фиксировано. Тогда по формуле nk (k1, k2, …, kn) = 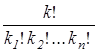получим |M| = 28 (4,4) = = 70 по-разному раскрашенных кубов. Так как нам нужно раскрасить вершины в два цвета (4 - в красный, 4 - в синий), то минимальное количество циклов в перестановке должно быть равно двум. Поэтому все перестановки 1) – 24) (задача 1) имеют неподвижные точки. В результате в группе G имеется:

1 перестановка типа <1, 1, 1, 1, 1, 1, 1, 1>,

6 перестановок типа <4, 4>,

9 перестановок типа <2, 2, 2, 2>,

8 перестановок типа <1, 1, 3, 3>.

Тогда перестановка типа <1, 1, 1, 1, 1, 1, 1, 1> имеет 28 (4,4) = = 70 неподвижных точек. Каждая перестановка типа <4, 4> имеет (по принципу умножения Р2 =2∙1= 2 неподвижные точки. Для каждой перестановки типа <2, 2, 2, 2> имеется 24 (2, 2) = 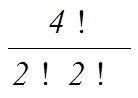= 6 неподвижных точек. Каждая перестановка типа <1, 1, 3, 3> имеет (по принципу умножения) Р2 =2∙1∙2∙1= 4 неподвижные точки. По лемме Бернсайда получаем (1∙70+ 6∙2 + 9∙6 + 8∙4) = 7.

 Скачать реферат