Мультипликативность стационарного распределения в открытых сетях с многорежимными стратегиями обслуживания

Докажем, что стационарное распределение изолированного узла в фиктивной окружающей среде имеет форму (2.2.15), (2.2.16). Полагая в (2.2.10) получим:

откуда получаем

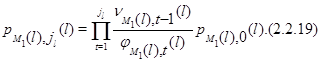
Из (2.2.9) для <

img width=89 height=24 src="images/referats/11207/image230.png">находим, что

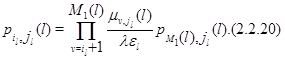
Для таких же из (2.2.9) также следует, что

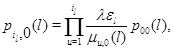
в частности,

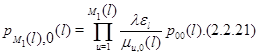
Подставляя (2.2.21) в (2.2.19), а затем подставляя полученное равенство в (2.2.20), будем иметь для

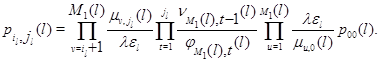
Тем самым доказано (2.2.15).

Для из (2.2.9) следует, что

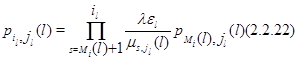
Полагая в (2.2.10) , получим:

откуда

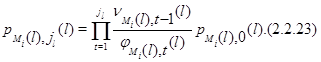
Далее, из (2.2.9)

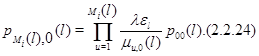
Подставляя (2.2.24) в (2.2.23), а затем полученное равенство в (2.2.22), для будем иметь

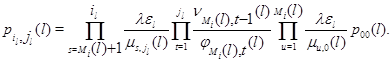
Таким образом, (2.2.16) доказано.

Наконец, (2.2.17) следует из того, что сумма всех стационарных вероятностей равна единице:

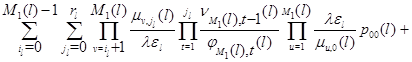
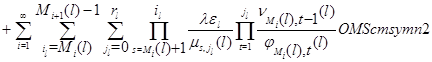
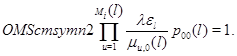
Достаточность сходимости ряда (2.2.14) для эргодичности вытекает из теоремы Фостера . Лемма 2.4 доказана полностью.

Основной результат 2.2 заключается в следующем.

Теорема 2.2. [45, C.184] Для выполнения (2.2.8) необходимо и достаточно, чтобы в нетерминальных узлах выполнялись условия (2.2.12), (2.2.13). При выполнении этого условия для эргодичности марковского процесса , описывающего поведение сети, достаточно, чтобы сходился ряд

где

При этом в нетерминальных узлах стационарное распределение процесса имеет форму (2.2.15) – (2.2.17).

Д о к а з а т.е. л ь с т в о. В для открытых сетей с «заявкосохраняющими» узлами установлено, что для мультипликативности стационарного распределения необходимо и достаточно, чтобы нетерминальные узлы являлись квазиобратимыми. Поэтому, с учетом условия квазиобратимости (2.1.16) для изолированного узла, которое в силу леммы 2.4 для узла с номером принимает форму (2.2.12), (2.2.13) имеет место первое утверждение теоремы.

Докажем, что при выполнении условия (2.2.25) процесс эргодичен. Как отмечалось ранее, неприводим. Остается воспользоваться эргодической теоремой Фостера , согласно которой достаточно проверить, что система уравнений

где – интенсивность перехода из состояния в состояние ; , определяемая посредством (2.2.26), – интенсивность выхода из состояния , имеет нетривиальное решение такое, что . Действительно, беря , где определяется (2.2.8), получим, что (2.2.27) превращаются в глобальные уравнения равновесия для сети, которым удовлетворяет. А ряд сходится, так как его члены отличаются от членов ряда (2.2.25) постоянным множителем.

Замечание 2.3. Отметим, что для эргодичности марковского процесса достаточно потребовать выполнения следующих двух условий, гарантирующих сходимость ряда (2.2.25):

для всех

1) сходятся ряды

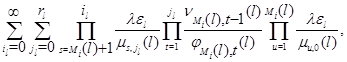
Здесь условие 2) гарантирует регулярность марковского процесса, который не может за конечное время делать бесконечное число скачков из одного состояния в другое.

Замечание 2.4. Если условия (2.2.12), (2.2.13) выполнены во всех узлах и ряд (2.2.25) сходится, то получается простой алгоритм для нахождения стационарных вероятностей:

1. Решается система линейных уравнений (2.2.1).

2. Проверяется выполнение условий (2.2.12), (2.2.13).

3. Определяется по формуле (2.2.26) и проверяется сходимость ряда (2.2.25).

4. Определяются с помощью соотношений (2.2.15) – (2.2.17).

5. Находится стационарное распределение состояний сети с помощью формулы (2.2.8).

При этом нормировку вероятностей можно производить не раз, как это делалось в пункте 4, а один раз, исходя из условия . Отметим также, что если в сети есть терминальные узлы, в которых условия (2.2.12), (2.2.13) не выполняются, то алгоритм существенно усложнится, так как в этих узлах нельзя применить (2.2.15) – (2.2.17). Поэтому для таких узлов необходимо добавить процедуру численного решения системы уравнений (2.2.2) – (2.2.7) с последующей его нормировкой.

 Скачать реферат