Расчет жесткого стержня

1. Задание

Построить математическую модель расчета опорных реакций жесткого стержня с тремя опорными узлами и определение внутренних усилий, поперечной силы Q и изгибающего момента М, возникающих во внутренних сечениях стержня под действием нагрузки. Разработать алгоритм и составить программу вычисления опорных реакций и распределения вдоль оси стержня внутренних усилий.

Вариан

т - 82-4г. Схема - 2.

Численный метод решения СЛАУ - метод Гаусса.

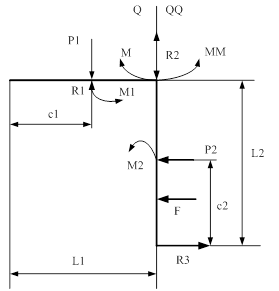
2. Схема нагруженного стержня

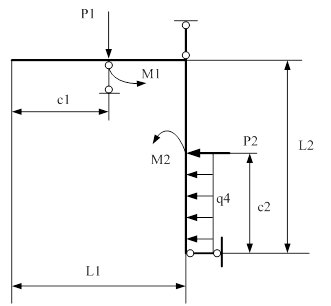
q4 - интенсивность распределенной нагрузки, H/м

C1, C2 - отрезок балки, м

L1, L2 - пролет балки, м

М1, M2 - круговой момент, Hм

3. Исходные данные

P1=15kH P2=30kH L1=6м L2=12м

M1=10kHм M2=35kHм С1=3м C2=2м

L1=6м L2=12м q4=10kH

4. Построение системы линейных алгебраических

уравнений для определения опорных реакций.

Преобразуем исходную систему:

отбросим опорные стержни и заменим их опорными

реакциями (R1; R2; R3)

интенсивность распределённой нагрузки заменим эквивалентной

силой (F4 = q4c2)

зададим систему координат.

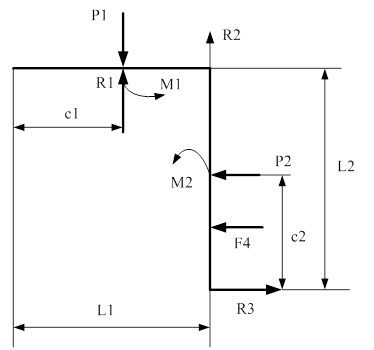
Для вывода формул вычисления опорных реакций запишем уравнение равновесия стержня: сумма моментов относительно опорной точки стержня равна нулю.

:

Представил уравнения равновесия балки в форме системы линейных алгебраических уравнений (СЛАУ).

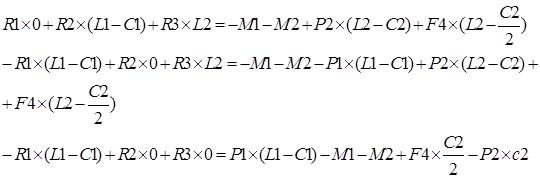
Матричная форма записи СЛАУ вычисление опорных реакций балки

AR=B

А - матрица коэффициентов при неизвестных

R - матрица неизвестных

В - матрица свободных членов

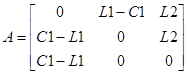
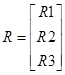
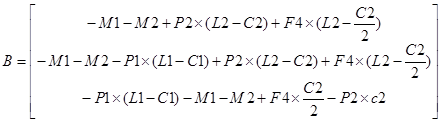
5. Вывод формул проверки, достоверности вычисления опорных реакций

Для проверки правильности вычисления опорных реакций использовал уравнения равновесия балки, сумма проекций всех сил действующих на балку равна нулю.

Y=R1-P1+R2=0

X=R3-P2-F4=0

6. Вывод рабочих формул определение внутренних усилий стержня

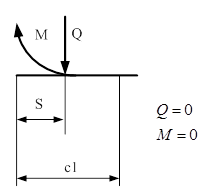
На рассматриваемом стержне выделим четыре участка длиной S (длина отрезка от начала до точки сечения стержня), для которых составим формулы для вычисления внутренних усилий: поперечной силы Q и изгибающего момента М.

s - отрезок от начала до точки сечения балки

I cечение

II cечение

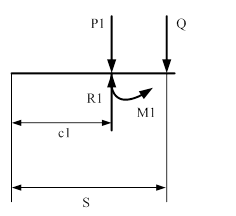
III cечение

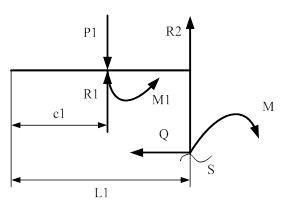
IV cечение

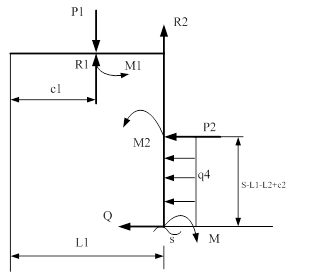
В точках границ , ,организуем вычисления поперечной силы Q слева (и QQ справа), изгибающего момента М слева (и MМ справа) от рассматриваемых точек.

1 точка границ:

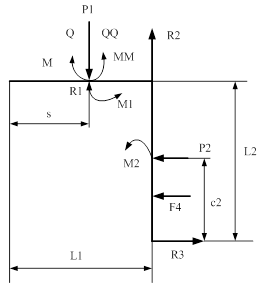
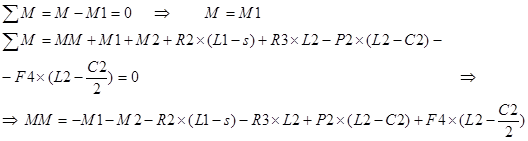
2 точка границ:

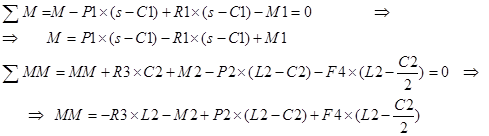
3 точка границ:

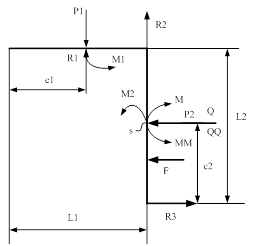
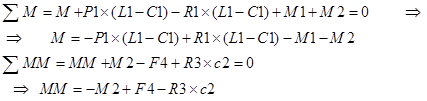
7. Численный метод решения СЛАУ - метод Гаусса

Численный метод Гаусса относится к точным методам решения системы линейных алгебраических уравнений. Он основан на приведении матрицы коэффициентов к треугольному виду. Процесс поиска решения системы линейных алгебраических уравнений выполняется в два хода: прямой ход и обратный ход.

Прямой ход исключения переменных выполняется путём преобразования коэффициентов СЛАУ, коэффициенты при неизвестных обращаются в нуль, начиная со второго по формулам:

; ; , где

; ;

 Скачать реферат