Математические основы теории систем

I-часть

Задание1: По виду электрической схемы построить математическую модель объекта управления в пространстве состояния.

Задание2: По построенной модели составить структурную схему и сигнальный граф.

Задание3: Используя формулу Мейсона найти передаточную функцию объекта управления.

Задание4: По передаточной функции объекта управления определить временные

и частотные характеристики. Построить их зависимость: АЧХ, ФЧХ.

Задание5: По полученным зависимостям определить прямые и косвенные оценки качества объекта управления.

II-часть.

Задание1: По заданной корреляционной функции Kx(t) определить спектральную плотность Sx(w) для белого шума, который подается на вход формирующего фильтра.

Задание2: По заданным статистическим характеристикам Se,Sv определить передаточную функцию формирующего фильтра y(р)

Задание3: Представить объект управления в виде

V(t) X(t) Y(t)

и оценить качество полученной системы по переходной характеристике.

Задание4: Сделать вывод по работе.

I-часть

Данные

L1 e(t) L2

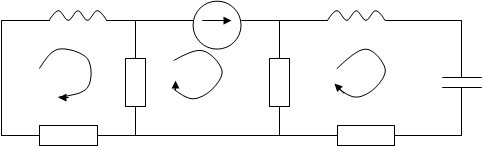
1. Построить математическую модель объекта управления в пространстве состояния.

В схеме три элемента, запасающих энергию: , следовательно, математическая модель должна быть третьего порядка.

2. Построение математической модели.

Задаемся направлением контурных токов . Составляем три уравнения по второму закону Кирхгофа для контуров:

(1)

(2)

(3)

В уравнении (3) есть интеграл, поэтому дифференцируем его:

(3*)

В уравнениях (3*), (2), (3) есть производные, в качестве выбираем элементы с производными и производные берем на порядок ниже:

(4)

(5)

(6)

Запишем введенный вектор состояния в виде дифференциальных уравнений первого порядка.

Уравнение в пространстве состояний записывается в левой части:

В полученных уравнениях имеется шесть переменных . Необходимо уйти от , выразив их через

Из выражения (1) выразим :

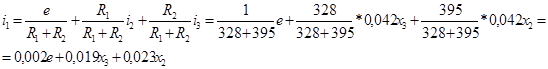
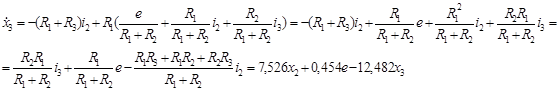
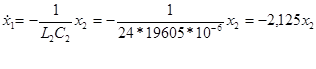
Получили три дифференциальных уравнения и одно уравнение для выходного параметра.

Запишем полученную систему уравнений в матричном виде:

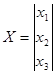
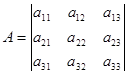
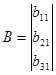
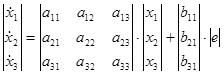
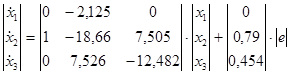
Получим матричное уравнение для выходной переменной:

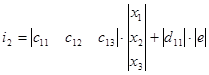
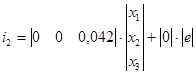
2. Построение сигнального графа.

Перепишем уравнения в общем, виде для построения графа системы:

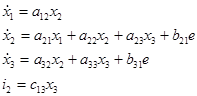
Построение графа произведем в два шага:

Шаг 1. Ставим точки входа, выхода системы и векторы параметров

Шаг 2. Соединяем все параметры связями согласно системе уравнений.

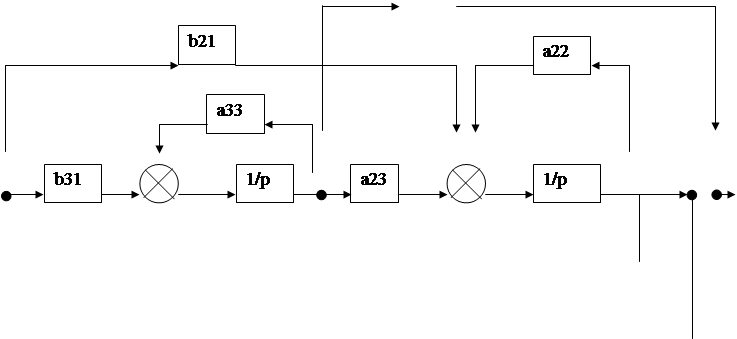
e X 3 X 3 X 2 X 2 i2

		a21

 Скачать реферат