Применение магнетронных генераторов большей мощности в радиолокационных системах

Используем уравнение, определяющее фазовую скорость волны -вида -й пространственной гармоники. Чтобы получить условие усредненного синхронизма между электронами и волной, вместо радиуса анода rа подставим средний радиус пространства взаимодействия, равный

dth=79 height=41 src="images/referats/11147/image006.png">. (1.1)

Таким образом, средняя фазовая скорость волны в пространстве взаимодействия составляет:

. (1.2)

Средняя скорость движения электронов равна . Отсюда условие синхронизма может быть записано в виде:

. (1.3)

В рассматриваемой системе напряженность постоянного электрического поля можно выразить в виде Подставляя эту величину в предыдущее уравнение и учитывая, что генерируемая частота определяется в основном резонансной частотой данного вида колебаний, т.е. что , имеем:

(1.4)

Согласно этому уравнению анодное напряжение, при котором должно происходить самовозбуждение многорезонаторного магнетрона, для каждого вида колебаний при фиксированном номере гармоники линейно связано с индукцией магнитного поля. Отношение есть величина постоянная для данного магнетрона при заданных значениях и .

На рисунке 1.3, а построены соответствующие графики для трех видов колебаний 8-резонаторного магнетрона при Здесь же построена парабола критического режима.

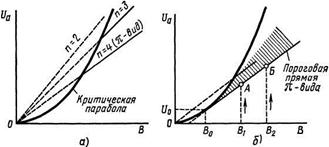
Рисунок 1.3 - Самовозбуждение магнетрона: а ) – для упрощенного случая при N=8, б)– для -вида колебаний

Прямые, определяемые уравнением (1.4), проходят через начало координат и пересекают критическую параболу. С физической точки зрения понятно, что при генерация колебаний типа бегущей волны невозможна: все электроны попадают на анод не позднее чем через половину периода циклоидального колебания. Поэтому условиям самовозбуждения отвечают лишь участки прямых, выделенные на рисунке 1.3, а сплошными линиями и лежащие ниже параболы критического режима.

Рассмотренные графики самовозбуждения не могут претендовать на большую точность, а можно лишь установить, что для каждого вида колебаний существуют оптимальные соотношения между постоянным анодным напряжением и индукцией магнитного поля. Это не означает, однако, что генерирование колебаний невозможно в точках плоскости (f/a, В), не лежащих на указанных прямых. Если увеличивать анодное напряжение при неизменной индукции магнитного поля, то генерируемая мощность на данном виде колебаний должна переходить через максимум и уменьшаться при удалении от прямой, определяемой уравнением (1.4). При дальнейшем увеличении напряжения £/а могут быть достигнуты условия синхронизма с полем волны следующего вида, имеющего более низкий номер п. Естественно предположить, что существует промежуточная область неустойчивой генерации, где небольшие изменения анодного напряжения и постоянного анодного тока приводят к скачкообразному переходу с одного вида колебаний на другой.

Отвлекаясь от возбуждения колебаний на пространственных гармониках, отметим, что -вид колебаний требует для своего возбуждения наименьшего анодного напряжения. Это свойство -вида играет большую роль, особенно при работе магнетронов в импульсном режиме. Одновременно можно сделать вывод, что -вид отделен от других видов колебаний не только по частоте, но и по величине анодного напряжения.

1.3 К.П.Д. магнетрона

Трудности, связанные с прямым вычислением отдаваемой электронами мощности, настолько велики, что в настоящее время не существует строгого расчета электронного к. п. д. магнетрона типа бегущей волны. В подобных случаях можно вычислить мощность, рассеиваемую электронами после взаимодействия с полем, и затем использовать закон сохранения энергии

Рассмотрим кинетическую энергию, которую имеет электрон в момент удара об анод после того, как значительная часть потенциальной энергии электрона отдана высокочастотному полю в пространстве взаимодействия.

При обсуждении процессов сортировки электронов было показано, что циклоидальная траектория благоприятного электрона при малой амплитуде высокочастотных колебаний наклоняется в сторону анода, но остается в основном такой же, как в статическом режиме. Радиус катящегося круга в плоском магнетроне равен

, (1.5)

где - расстояние между катодом и анодом.

Скорость, которую имеет электрон при ударе об анод, зависит от момента удара. Будем исходить из наихудшего с точки зрения величины к. п. д. случая, когда удар происходит в верхней точке циклоидальной траектории. Полюсом вращения является точка касания круга к плоскости, по которой происходит качение этого круга. Радиус вращения электрона равен здесь . Зная угловую скорость вращения круга нетрудно получить максимальную скорость электрона:

. (1.6)

К такому же результату можно придти, исходя из известной скорости центра круга, равной .

Максимальная кинетическая энергия, рассеиваемая электроном на аноде, равна

(1.7)

Тот же электрон, находясь на катоде до начала движения в пространстве взаимодействия, обладал по отношению к аноду потенциальной энергией, равной Wn = eUa, при нулевой кинетической энергии. Следовательно, энергия, отданная высокочастотному полю, по закону сохранения энергии равна Wn —.

К. п. д. рассматриваемого одиночного электрона, таким образом, имеет величину

(1.8)

 Скачать реферат