Методика формирования умений решать тригонометрические уравнения и неравенства в курсе алгебры и начал анализа

3. Отметьте на тригонометрической окружности точки , если:

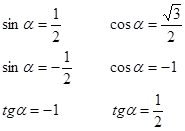
4. Приведите выражение к тригонометрическим функциям I четверти.

а) б) rc="images/referats/7508/image294.png">в)

5. Дана дуга МР. М – середина I – ой четверти, Р – середина II-ой четверти.

Ограничить значение переменной t для: (составить двойное неравенство)

а) дуги МР;

б) дуги РМ.

6. Записать двойное неравенство для выделенных участков графика:

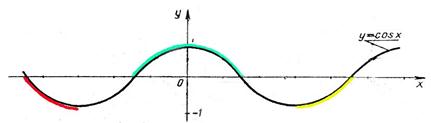
7. Решите неравенства sinx > 1, sinx <-1 , cos x > 1, cosx <-1

8. Преобразовать выражение sin5xcos4x-cos5xsin4x

Обратим внимание на задания 5 и 6. Естественно, именно оно лежит в основе решения простейшего тригонометрического неравенства.

Неравенства, характеризующие дугу, мы предлагаем составлять в 2 шага. На первом шаге составляем «ядро» записи неравенства (это, собственно говоря, главное к чему следует научить школьников); для заданной дуги МР получим . На втором шаге составляем общую запись:

, .

Если же речь идёт о дуге РМ, то при записи «ядра» нужно учесть, что точка А(0) лежит внутри дуги, а потому к началу дуги нам приходиться двигаться по первой отрицательной окружности. Значит, ядро аналитической записи дуги РМ имеет вид , а общая запись имеет вид. ,

При решении задания 7, следует особо обратить внимание на значимость свойств тригонометрических функций.

На втором этапе обучения решению тригонометрических неравенств можно предложить следующие рекомендации, связанные с методикой организации деятельности учащихся. При этом будем ориентироваться на уже имеющиеся у учащихся умения работать с тригонометрической окружностью или графиком, сформированные во время решения простейших тригонометрических уравнений.

Во-первых, мотивировать целесообразность получения общего приема решения простейших тригонометрических неравенств можно, обратившись, например, к неравенству вида . Используя знания и умения, приобретенные на подготовительном этапе, учащиеся приведут предложенное неравенство к виду; , но могут затрудниться в нахождении множества решений полученного неравенства, т.к. только лишь используя свойства функции синус решить его невозможно. Этого затруднения можно избежать, если обратиться к соответствующей иллюстрации (решение уравнения графически или с помощью тригонометрического круга).

Во-вторых, учитель должен обратить внимание учащихся на различные способы выполнения задания, дать соответствующий образец решения неравенства и графическим способом и с помощью тригонометрического круга.

Предлагаем такие варианты решения неравенства

1. Решение неравенства с помощью круга.

Решим тригонометрическое неравенство .

На первом занятии по решению тригонометрических неравенств предложим учащимся подробный алгоритм решения, который в пошаговом представлении отражает все основные умения, необходимые для решения неравенства.

Шаг 1. Начертим единичную окружность, отметим на оси ординат точку и проведем через нее прямую, параллельную оси абсцисс. Эта прямая пересечет единичную окружность в двух точках. Каждая из этих точек изображает числа, синус которых равен .

Шаг 2. Эта прямая разделила окружность на две дуги. Выделим ту из них, на которой изображаются числа, имеющие синус больший, чем . Естественно, эта дуга расположена выше проведенной прямой.

Шаг 3.Выберем один из концов отмеченной дуги. Запишем одно из чисел, которое изображается этой точкой единичной окружности .

Шаг 4. Для того чтобы выбрать число, соответствующее второму концу выделенной дуги, "пройдем" по этой дуге из названного конца к другому. При этом напомним, что при движении против часовой стрелки числа, которые мы будем проходить, увеличиваются (при движении в противоположном направлении числа уменьшались бы). Запишем число, которое изображается на единичной окружности вторым концом отмеченной дуги .

Таким образом, мы видим, что неравенству удовлетворяют числа, для которых справедливо неравенство . Мы решили неравенство для чисел, расположенных на одном периоде функции синус. Поэтому все решения неравенства могут быть записаны в виде

Внимательно рассмотрите рисунок и разберитесь, почему все решения неравенства могут быть записаны в виде

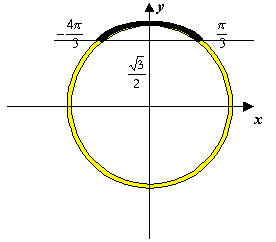
Обратить внимание учащихся на то, что при решении неравенств для функции косинус, прямую проводим параллельно оси ординат.

1. Графический способ решения неравенства.

Строим графики и , учитывая, что

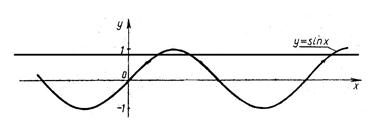
Затем записываем уравнение и его решение , найденное с помощью формул .

(Придавая n значения 0; 1; 2, находим три корня составленного уравнения). Значения являются тремя последовательными абсциссами точек пересечения графиков и . Очевидно, что всегда на интервале () выполняется неравенство , а на интервале () – неравенство . Нас интересует первый случай, и тогда добавив к концам этого промежутка число, кратное периоду синуса, получим решение неравенства в виде: ;

 Скачать реферат