Экспоненциальный фильтр
Цель работы
Ознакомиться с аналоговым и дискретным вариантами реализации фильтра
Общие сведения
В аналоговом варианте экспоненциальный фильтр представляет собой апериодическое звено и описывается дифференциальным уравнением
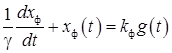 , (15)
, (15)
где ![]() и
и ![]() – параметры настройки фильтра.
– параметры настройки фильтра.
Уравнению (15) соответствует амплитудно-фазовая характеристика (АФХ)
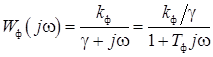 , (16)
, (16)
где 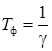 – постоянная времени фильтра.
– постоянная времени фильтра.
Из условия (3) ![]() (математическое ожидание) для статического режима определяют оптимальное значение параметра
(математическое ожидание) для статического режима определяют оптимальное значение параметра ![]() . Коэффициент усиления
. Коэффициент усиления
![]() . (17)
. (17)
Определение оптимального значения параметра ![]() производится из условия (4)
производится из условия (4) ![]() (среднеквадратичная погрешность оценки).
(среднеквадратичная погрешность оценки).
Для этого предварительно рассчитывают спектральную плотность ![]() погрешности экспоненциального фильтра по формуле (7) с учётом (16) и (17).
погрешности экспоненциального фильтра по формуле (7) с учётом (16) и (17).
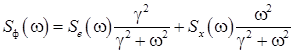 . (18)
. (18)
Дисперсия погрешности экспоненциального фильтра, согласно (6), (7), с учётом (16), равна
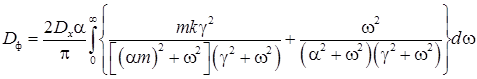 . (19)
. (19)
При вычислении этого интеграла оба слагаемых подынтегрального выражения раскладывают на простые дроби, каждая из которых сводится к табличному интегралу вида
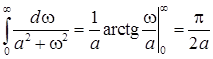 . (20)
. (20)
После выполнения соответствующих преобразований получают следующее выражение для дисперсии погрешности фильтрации:
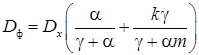 . (21)
. (21)
Оптимальное значение параметра настройки ![]() получают из необходимого условия экстремума функции
получают из необходимого условия экстремума функции ![]() :
:
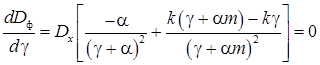 . (22)
. (22)
Откуда оптимальное значение параметра
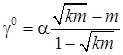 . (23)
. (23)
Таким образом, функция ![]() имеет единственную точку стационарности, тип которой зависит от знака второй производной при
имеет единственную точку стационарности, тип которой зависит от знака второй производной при ![]() .
.
Можно показать, что при выполнении условия
![]() , (24)
, (24)
особая точка является минимумом функции ![]() , а при выполнении условия
, а при выполнении условия
![]() (25)
(25)
в точке ![]() , функция
, функция ![]() достигает максимума.
достигает максимума.
Таким образом, если сочетание характеристик полезного сигнала и помехи соответствуют случаю (24), то оптимальное значение параметра настройки ![]() определяется по формуле (23).
определяется по формуле (23).
Если это условие не выполняется, то оптимальным является наибольшее допустимое значение параметра ![]() .
.
При программной реализации экспоненциального фильтра дифференциальное уравнение (15) заменяют разностным уравнением вида
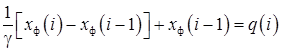 (26)
(26)
где i – номер цикла расчёта
Отсюда получают следующее рекуррентное соотношение для вычисления сглаженного значения ![]() в очередном i-том цикле расчёта:
в очередном i-том цикле расчёта:
![]() (27)
(27)
К достоинствам алгоритма экспоненциальной фильтрации относятся: малая трудоёмкость расчётов и малый объём памяти ЭВМ, в которой должны храниться величина ![]() и обновляемая в каждом цикле расчёта величина
и обновляемая в каждом цикле расчёта величина ![]() .
.
Пример выполнения лабораторной работы с использованием пакета MCAD представлен в Приложении 3 к лабораторной работе №2. Здесь представлен вариант расчёта трёхкратного сглаживания экспериментальных данных, полученных от ИИК технологического процесса, построены графики.
Общая часть заданий
1. Ознакомиться с теоретическим описанием
2. Выполнить расчёты в MCAD сглаженных значений данных полученных от ИИК. Для расчётов пользоваться формулами:
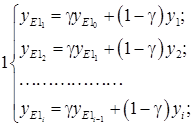
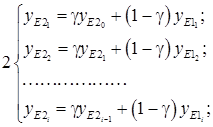
![]()
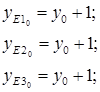
За начало отсчёта примем следующие допущения:
Расчёт произвести для трёх значений g:
g = 0,4; 0,5; 0,6
3. Провести анализ полученных зависимостей на выполнение фильтрации полезного сигнала от помехи
4. Сделать выводы и дать предложения о возможности применения сглаживающего фильтра для уменьшения помех
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
