Методика формирования умений решать тригонометрические уравнения и неравенства в курсе алгебры и начал анализа

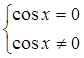или

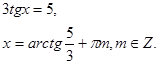
2.

Сгруппируем соответствующие слагаемые, получим:

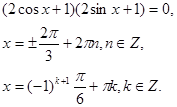
1.4.6 Уравнения вида 2 src="images/referats/7508/image106.png">

Один из способов решения такого уравнения состоит в том, что левую часть уравнения можно преобразовать по формуле:

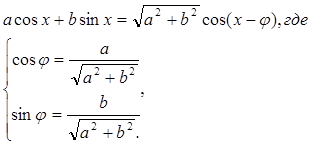
Примеры:

1.

;

, т.к. это решение системы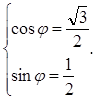

Подставляя в формулу, получаем:

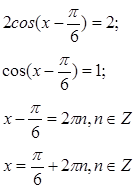
2.

, т.к. это решение системы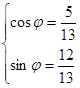

Подставляя в формулу, получаем

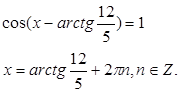
К сожалению, внимание учащихся нечасто обращается на преобразование выражения .

В некоторых пособиях эта формула приведена в таком виде

где .

Такая запись приведёт к ошибке, если, например, a и b отрицательны.[10]

Выделенные виды тригонометрических уравнений представлены в пособиях по математике для средней школы. Значит, перед учителем стоит задача – формировать у учащихся умения решать уравнения каждого вида.

1.5 Тригонометрические неравенства и методы их решения

1.5.1 Решение простейших тригонометрических неравенств

Большинство авторов современных учебников по математике предлагают начать рассмотрение данной темы с решения простейших тригонометрических неравенств. Принцип решения простейших тригонометрических неравенств основан на знаниях и умениях определять на тригонометрической окружности значения не только основных тригонометрических углов, но и других значений.

Между тем, решение неравенств вида , , , можно осуществлять следующим образом: сначала находим какой-нибудь промежуток (), на котором выполняется данное неравенство, а затем записываем окончательный ответ, добавив к концам найденного промежутка число кратное периоду синуса или косинуса: (). При этом значение находится легко, т.к. или . Поиск же значения опирается на интуицию учащихся, их умение заметить равенство дуг или отрезков, воспользовавшись симметрией отдельных частей графика синуса или косинуса. А это довольно большому числу учащихся иногда оказывается не под силу. В целях преодоления отмеченных трудностей в учебниках в последние годы применялся разный подход к решению простейших тригонометрических неравенств, но улучшения в результатах обучения это не давало.

Мы на протяжении ряда лет для нахождения решения тригонометрических неравенств довольно успешно применяем формулы корней соответствующих уравнений.

Изучение данной темы осуществляем таким образом:

1. Строим графики и у = а, считая, что .

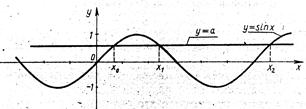
Затем записываем уравнение и его решение . Придавая n 0; 1; 2, находим три корня составленного уравнения: . Значения являются абсциссами трёх последовательных точек пересечения графиков и у = а. очевидно, что всегда на интервале () выполняется неравенство , а на интервале () – неравенство .

Добавив к концам этих промежутков число, кратное периоду синуса, в первом случае получим решение неравенства в виде: ; а во втором случае – решение неравенства в виде:

2. Далее проводим аналогичные рассуждения для косинуса

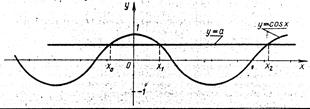
Только в отличие от синуса из формулы , являющейся решением уравнения , при n = 0 получаем два корня , а третий корень при n = 1 в виде . И опять являются тремя последовательными абсциссами точек пересечения графиков и . В интервале () выполняется неравенство , в интервале () – неравенство

 Скачать реферат