Производная и ее применение для решения прикладных задач

3.6 Разложение на множители и упрощение выражений.

Пример 1.

Разложить на множители выражение

.

Решение:

Считая х переменной величиной, рассмотрим функцию . Имеем .

Так как width=487 height=24 src="images/referats/7475/image108.png">,

то отсюда заключаем, что

.

Получаем , где С не зависит от х, но зависит от y и z.

Так как последнее равенство верно при любом х, то, полагая, например, в нем х=0 и учитывая, что , найдем .

Таким образом,

Итак, =.

Пример 2.

Упростить выражение

Решение

Считая х переменной величиной, рассмотрим функцию

Тогда, дифференцируя ее, имеем

.

Отсюда находим, что , где С не зависит от х, но может зависеть

от y и z. Полагая, например, х=0, получаем

.

Поскольку , то С=0.

Следовательно, .

3.7 Вычисление суммы

Пример 1.

Найти сумму

Решение:

Пусть .

Так как

,

, то

.

Поскольку есть сумма первых членов геометрической прогрессии со знаменателем х, , то

.

Так как , то

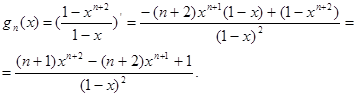
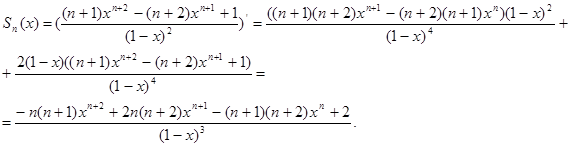
3.8 Сравнение чисел и доказательство неравенств

При доказательстве неравенств или для сравнения двух чисел полезно перейти к общему функциональному неравенству.

Пример 1.

Сравнить и .

Решение.

Рассмотрим функцию .

Так как

,

,

То функция возрастает на интервале .

Таким образом,

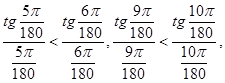
И, следовательно, <.

Пример 2.

Какое из чисел больше: или ?

Решение.

Рассмотрим функцию Так как и при то функция возрастает на множестве всех действительных чисел. Поэтому , т.е.

Пример 3.

Докажите, что при .

Доказательство:

Рассмотрим функцию при и .

При , .

Находим и :; ;

;

. В точке =6, то есть имеет минимум, равный . При функция убывает от до , а при , то есть функция возрастает. При , что и доказывает неравенство.

3.9 Решение неравенств

Пример 1.

.

Решение

Найдем участки возрастания и убывания функции . Производная этой функции равна . Так как дискриминант квадратного трехчлена является отрицательным числом и коэффициент при этого квадратного трехчлена больше нуля, то для каждого действительного х имеем неравенство .

 Скачать реферат