Производная и ее применение для решения прикладных задач

По правилу Лопиталя

Далее, элементарным путем находим:

3.15 Решение физических задач, связанных с нахождением скорости, ускорения и т.д.

Пример 1.

Дано уравнение прямолинейного движения тела: , где S- путь, пройденный телом, м; t- время, с. Найдите скорость тела в момент времени t=1 c.

Решение.

Скорость это производная пути по времени. Значит:

Подставив значение времени получим:

Пример 2.

Точка движется по закону . Найти скорость и ускорение через 2 с после начала движения (движение считать прямолинейным).

Решение.

Скорость это производная пути по времени. Значит: .

Подставив значение времени получим

Пример 3.

Тело движется прямолинейно по закону Найти его кинетическую энергию через 5 с после начала движения, если масса тела 3 кг.

Решение.

Формула нахождения кинетической энергии: .

Найдем скорость тела. , .

Кинетическая энергия тела составит: .

3.16 Решение экономических задач

Пример 1.

Выбрать оптимальный объем производства фирмой, функция прибыли которой может быть смоделирована зависимостью:

π(q) = R(q) - C(q) = q2 - 8q + 10

Решение:

π'(q) = R'(q) - C'(q) = 2q - 8 = 0 → qextr = 4

При q < qextr = 4 → π'(q) < 0 и прибыль убывает

При q > qextr = 4 → π'(q) > 0 и прибыль возрастает

При q = 4 прибыль принимает минимальное значение.

Каким же будет оптимальный объем выпуска для фирмы? Если фирма не может производить за рассматриваемый период больше 8 единиц продукции (p(q = 8) = p(q = 0) = 10), то оптимальным решением будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и / или оборудования. Если же фирма способна производить больше 8 единиц, то оптимальным для фирмы будет выпуск на пределе своих производственных мощностей.

Пример 2.

Кривая спроса задана выражением , где - объем продаж; - цена товара в условных единицах. Объем продаж составляет 10 000. Определите, каким должно быть изменение цены товара, чтобы объем продаж возрос на 1%.

Решение.

Определим цену , соответствующую объему продаж

Для оценки изменения цены товара воспользуемся формулой приближенных вычислений По условию задачи составляет 1% от 10000 или 10000/100=100. Найдем значение

Тогда Таким образом, для увеличения объема продаж на 1% цена товара должна быть снижена приблизительно на 0,105 у.е.

3.17 Разложение функций в ряд с помощью формулы Тейлора

1) Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно.(Т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности).

2) Пусть х- любое значение из этой окрестности, но х  а.

Тогда между точками х и а найдется такая точка , что справедлива формула:

- это выражение называется формулой Тейлора, а выражение:

называется остаточным членом в форме Лагранжа.

При получаем формулу Маклорена:

где ,

Пример 1.

Многочлен разложить по целым положительным степеням бинома х-2.

Решение.

Отсюда:

Следовательно, или

Пример 2.

Функцию разложить по степени бинома х+1 до члена, содержащего

Решение

для всех n, Следовательно ,

где

Пример 3

Разложить функцию 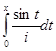в ряд Маклорена.

Решение.

Как известно, этот интеграл нельзя выразить через элементарные функции. Для отыскания разложения данного интеграла в ряд Маклорена необходимо разложить подынтегральную функцию в степенной ряд, а затем почленно проинтегрировать (степенной ряд сходится равномерно на любом отрезке, лежащем внутри промежутка сходимости, поэтому его можно проинтегрировать почленно).

3.18 Задача о линеаризации функции

По всей вероятности, исторически задача стояла так: «Написать уравнение касательной к графику функции в точке с абсциссой ». Дело в том, что ученым (в частности вычислителям) надо было в случае довольно «громоздкой» зависимости между переменными заменить в окрестности некоторой точки эту зависимость более простой. А самой простой является линейная зависимость. Поэтому вместо сформулированной выше задачи выдвинулись требования: «Заменить данную функцию линейной функцией в окрестности точки ». Эта идея занимала Тейлора. В случае, если эта замена давала вычислителям большие погрешности, ставилась задача замены данной функции в окрестности точки квадратичной функцией, многочленом третьей степени, четвертой и т.д.- до тех пор, пока не получалась нужная точность вычислений. Эта идея имеет простой геометрический смысл: при замене данной функции линейной в окрестности точки рассматривается касательная , при замене квадратичной- соприкасающаяся парабола, при замене многочленом третьей степени- соприкасающаяся кубическая парабола и т.д.

 Скачать реферат