Сущность метода Монте-Карло и моделирование случайных величин

Разыгрывать значение можно следующим образом:

1) выбираются два значения и случайной величины и строится случайная точка ight=21 src="images/referats/7462/image088.png">с координатами

2) если точка лежит под кривой , то полагаем , если же точка лежит над кривой , то пара отбрасывается и выбирается новое значение.

1.2 Вычисление интегралов

Рассмотрим функцию , заданную на интервале , требуется приближенно вычислить интеграл

(2.1)

Этот интеграл может быть несобственным, но абсолютно сходящимся.

Выберем произвольную плотность распределения , определённую на интервале . Наряду со случайной величиной , определённой в интервале с плотностью , необходимо определить случайную величину

Согласно соотношению получим

Рассмотрим теперь одинаковых независимых случайных величин и применим к их сумме центральную предельную теорему. Формула (1.7) в этом случае запишется так:

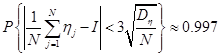
Последнее соотношение означает, что если выбирать значений , то при достаточно большом

(2.2)

Оно показывает также, что с очень большой вероятностью погрешность приближения (2.2) не превосходит .

Для расчёта интеграла (2.1) можно использовать любую случайную величину . Определённую в интервале с плотностью . В любом случае . Однако дисперсия , а с ней и оценка погрешности формулы (2.2) зависят от того, какая величина используется, так как

(2.3)

Докажем, что это выражение будет минимальным тогда, когда пропорциональна .

Для этого воспользуемся неравенством

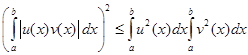, в которым положим , . Получим неравенство

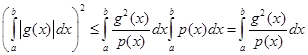(2.4)

Из (2.3), (2.4) следует, что

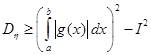(2.5)

Остается доказать, что нижняя граница дисперсии (2.5) реализуется при выборе плотности . Так как

.

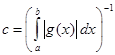Следовательно,

,

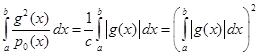и правая часть (2.3) обращается в правую часть (2.5)

Использовать плотность для расчёта практически невозможно, так как для этого нужно знать значение интеграла . А его вычисление представляет собой задачу, равноценную задаче о вычислении интеграла (2.1). Поэтому ограничиваются следующей рекомендацией: желательно, чтобы плотность была пропорциональна .

Конечно, выбирать очень сложные нельзя, так как процедуры разыгрывания станет очень трудоёмкой. Оценку (2.2) с плотностью , сходной , называют существенной выборкой.

Также если стоит задача вычислить интеграл (2.1), преобразуем его к виду

(2.6)

Если теперь обозначить (2.7)

То интеграл принимает вид

(2.8)

и может быть вычислен при помощи метода статистических испытаний.

В частном случае, если и конечны или их можно считать конечными приближенно, в качестве целесообразно выбрать равномерный закон распределения.

Как известно, плотность вероятности равномерного закона распределения в интервале равна:

(2.9)

Подставим в интеграл (2.6) значение из формулы (2.9) и получим:

 Скачать реферат