Фигуры постоянной ширины. Треугольник Рело
Построим пару параллельных прямых, касающихся треугольника Рело. Проведём ещё пару касательных, перпендикулярных первой паре. Фигура окажется "запертой" в квадрате и будет касаться каждой из его сторон. При вращении фигуры в квадрате она будет постоянно прилегать ко всем сторонам квадрата.
4.2 Очертание четырёхугольника
Наиболее известное свойство треугольника Рело – оч
ертание четырёхугольника сложенным вращением этого треугольник (рис.8).
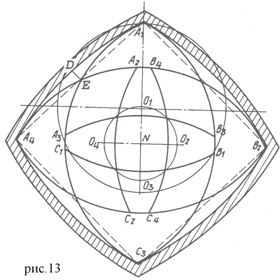
Если вращать треугольник А1В1С1 вокруг центра О1 описанной вокруг него окружности с радиусом О1А1, а центр треугольника О1 вращать в противоположную сторону в три раза быстрее по окружности с центром N, то треугольник очертит фигуру, которая незначительно отличается от четырёхугольника. А именно, за один оборот центра О1 направо по окружности с радиусом О1N два угла четырёхугольника будут оформлены вершиной А треугольника Рело и по одному – вершинами В и С, т.е. через каждую четверть оборота вокруг центра N треугольника Рело будет находиться в положении А2В2С2, А3В3С3 иА4В4С4.
Выполненные на рисунке построения показывают небольшую кривизну сторон четырёхугольника, о которой также указывают инженеры. По их данным, наибольшее отклонение стороны от идеальной прямой имеет место в середине стороны. Треугольник Рело при вращении контактирует с точкой D серединой своей стороны.
Обозначим через R- радиус, описанного около треугольника Рело круга, r=О1N. Тогда
А1В1=А2В2=А3В3=А4В4=R![]() ,
,
ND=r![]() R+R
R+R![]()
Из треугольника А1NА4 получаем
А1N=r![]() R, NЕ=
R, NЕ=![]()
Из равенства DE=ND=NE следует, что
DE= r – R + R![]() ,
,
DE=R(![]() 1
1![]() )+r(1
)+r(1![]() )
)![]() 0,025R+0,293r.
0,025R+0,293r.
Вычислив кривизну, получаем:
DE ~ 0.025R + 0.293r
Таким образом, отклонение DE стороны квадрата от сделанной прямой зависит, в первую очередь, от радиуса r и не может быть устранено, потому что R и r не могут равняться нулю.
4.3 Движение вершины и центра треугольника Рело
Попробуем построить траектории движения двух характерных точек треугольника Рело при качении его по плоской горизонтальной поверхности. Такими точками будут одна из вершин треугольника и его геометрический центр. Моделирование одного полного оборота треугольника Рело показано на рисунке.
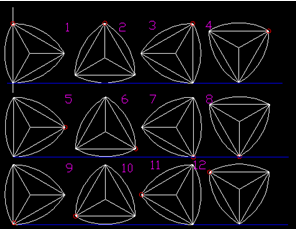
Рис.14
На фигурах 2, 6, 10 треугольник катится по поверхности окружности, на фигурах 4, 8, 12 треугольник переваливается через вершину, на остальных фигурах происходит смена характера движения треугольника с качения на переваливание и наоборот. Рассмотрим движение вершины треугольника. На фигурах 1, 2, 3 помеченная вершина движется линейно, по прямой (Рис. 10). Фактически помеченная вершина является центром вращения окружности, элементом которой является поверхность стороны треугольника Рело. На фигуре 3 помеченная вершина меняет траекторию движения с прямолинейной на траекторию движения по окружности с радиусом, равным длине стороны, по которой он движется на фигурах 3, 4, 5.
На фигуре 5 происходит смена траектории движения вершины. На фигурах 5, 6, 7 вершина движется по трохоиде точки, находящейся на поверхности окружности с радиусом, равным длине стороны треугольника. На фигурах 7, 8, 9 меченная вершина является точкой перевала треугольника, она жестко лежит на поверхности. Фигуры 9, 10, 11 – опять трохоида и 11, 12, 1 – движение по окружности. По аналогии эти фигуры описаны выше. Меченая вершина возвращается в исходную точку. Треугольник Рело совершил полный оборот.
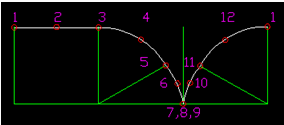
Рис.15 Движение вершины треугольника.
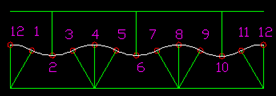
Рис.16 Движение центра треугольника.
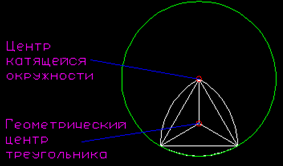
Рис.17
Очень важной является траектория движения геометрического центра треугольника. Если обозначить длину стороны треугольника через R, то расстояние от вершины до геометрического центра будет равно R/![]() . На фигурах 3 – 4 – 5, 7 – 8 - 9, 11 – 12 – 1 (Рис.16) центр движется по дугам с радиусом именно R/
. На фигурах 3 – 4 – 5, 7 – 8 - 9, 11 – 12 – 1 (Рис.16) центр движется по дугам с радиусом именно R/![]() . На фигурах же 1 – 2 – 3, 5 – 6 – 7, 9 – 10 – 11 центр движется по трохоиде, причем расстояние от центра катящейся окружности (не путать с геометрическим центром треугольника, Рис. 15) до траектории искомой точки опять же равно R/
. На фигурах же 1 – 2 – 3, 5 – 6 – 7, 9 – 10 – 11 центр движется по трохоиде, причем расстояние от центра катящейся окружности (не путать с геометрическим центром треугольника, Рис. 15) до траектории искомой точки опять же равно R/![]() .
.
4.4 Площадь треугольника Рело
Одна из задач моей работы: доказать, что из всех фигур постоянной ширины d треугольник Рело имеет наименьшую площадь.
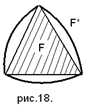
Для начала найдем площадь треугольника Рело:
![]()
![]() ;
;
![]() ;
;
![]()
Следовательно, площадь треугольника Рело равна
![]()
Попробуем доказать, что треугольник Рело имеет наименьшую площадь. Обозначим через n количество сторон многоугольника.
Пусть дан какой-то правильный n–угольник (с нечетным числом сторон), следовательно, его шириной будет наибольшая из диагоналей (в данном случае их две).
![]()
(при n![]()
![]() ),
), ![]() .
.
Оценим ![]() и площадь треугольника Релло:
и площадь треугольника Релло:
![]() ,
, ![]() >
>![]()
Следовательно, ![]() больше площади треугольника Рело, а равносторонний, треугольник является многоугольником с наименьшим числом вершин (сторон). Значит, с увеличением числа вершин многоугольника площадь фигуры постоянной ширины, в которую вписан этот многоугольник, будет увеличиваться.
больше площади треугольника Рело, а равносторонний, треугольник является многоугольником с наименьшим числом вершин (сторон). Значит, с увеличением числа вершин многоугольника площадь фигуры постоянной ширины, в которую вписан этот многоугольник, будет увеличиваться.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
