Передача данных в информационно-управляющих системах. Каналы передачи данных

Поясните, какие из перечисленных ошибок могут не обнаруживаться (7,4)-нециклическим кодом с тем же расстоянием. Приведите конкретные примеры таких ошибок.

Упражнение 3.9

На основе регистров сдвига постройте структурную схему декодера с исправлением однократных ошибок для укороченного (15,11)-циклического кода с минимальным расстоянием d0=3 и образующим многочленом g(x) = x4+x+1.

Нап

ишите несколько слов, принадлежащих данному коду. С их помощью проиллюстрируйте поведение декодера в условиях возникновения одно- и двукратных ошибок в кодовых словах.

Нужно ли что–нибудь изменить в схеме декодера с тем, чтобы он декодировал слова укороченного (14,10)-кода?

Рекомендации по решению задач РАЗДЕЛА 3

Задачи 3.1, 3.2, 3.3 преследуют цель дать некоторый тренаж в манипулировании с каноническими формами матриц G(n,k) и H(n,k).

Напомним, что в принципе роль порождающей матрицы G может выполнять любая совокупность из k линейно-независимых векторов длины n, попарные расстояния среди которых не меньше d0. Каноническая форма матрицы предполагает определенную технологию ее формирования. Матрица G представляет собой блочную структуру типа

G(n,k) = (I k | D k, n-k), (3.1)

где I k - единичная матрица размерности k;

D - блок дополнений размерности k*(n–k), каждая строка D i которого имеет вес w(Di)³(d0–1).

Проверочная матрица Н по определению ортогональна к G и структурно представляет собой

H(n,k) = ( Dт | I n–k ), (3.2)

где Dт - транспортированный блок D размерности k×(n–k);

In–k - единичная матрица размерности n–k.

Следствием ортогональности является

V*HТ = S = 0 (3.3)

- фундаментальное соотношение, лежащее в основе процедуры декодирования по синдрому S линейных (n,k)-кодов. Вектор V принадлежит коду G.

Матричная форма описания линейных кодов позволяет легко получить так называемые «укороченные коды» (задачи 3.1, 3.3). Укороченный (n–z,k–z) - код может быть получен из (n,k) - кода, если в канонической матрице G(n,k) вычеркнуть z строк сверху и z столбцов слева. В отношении помехоустойчивости такой код обладает свойствами неукороченного кода.

В задачах 3.7, 3.8, 3.9 обсуждаются циклические (n,k) - коды, получившие в практике передачи кодированных сигналов наибольшее распространение, благодаря прекрасным свойствам в отношении обнаружения ошибок и удивительно простой схемотехнике декодирующих устройств. В [1], [2 ], [3 ] приведены примеры построения структурных и функциональных схем кодирующих и декодирующих устройств.

В задачах 3.2, 3.4, 3.5, 3.6 требуется вычислять вероятности различных событий, связанных с возникновением в кодовом слове ошибок различных конфигураций. Построение формул для вычисления вероятностей можно освоить, например, с помощью [3]. Для этого только необходимо возобновить в памяти теоремы о сумме и произведении вероятностей для совместного наступления независимых событий, а также всякий раз четко формулировать суть события, вероятность наступления которого вычисляется.

С точки зрения инженерной практики наиболее правдоподобны задачи 3.2 и 3.4. Для данного источника предложить кодирование, помехоустойчивость которого удовлетворяет наперед заданным требованиям. В задаче 3.2 требуется, чтобы вероятность предъявления получателю неискаженной информации РНИ была не менее допустимого значения РНИ.ДОП. Исходим из того, что каждое сообщение отображается одним кодовым словом, а каждое слово передается однократно. Проделаем следующее:

1) закодируем источник неизбыточным кодом, определим k - длину неизбыточного слова;

2) проверим соотношение РНИ.НЕИЗБ = РНИ.ДОП. Скорее всего окажется, что РНИ.НЕИЗБ <Р НИ.ДОП. Если это не так, то неизбыточное кодирование решает задачу;

3) если вероятность предъявления получателю неискаженного сообщения меньше допустимого значения, то мы должны заключить, что понадобится код с исправлением ошибок в слове, так как при неизменном качестве двоичного канала РБ при однократной передаче слова других путей повышения этой вероятности нет;

4) определим максимальную кратность ошибки t, которая должна исправляться. Это легко сделать, если иметь в виду, что в обсуждаемом двоичном канале вероятность возникновения однократной ошибки равна

Cn1*PБ*(1–PБ)n–1; (3.4)

5) знание (или предложение) максимальной кратности исправляемой ошибки дает нам знание максимального расстояния кода, так как необходимо, чтобы d0=2t+1. Имеется в виду, что неравенство имеет минимальную глубину;

6) после этого можно вычислить число контрольных символов в кодовом слове, воспользовавшись известным теоретическим результатом (граница Хэмминга).

2(n–k) ³Cn0 + Cn1 + .+ Cnt. (3.5)

Здесь Cni - биномиальный коэффициент.

Убедимся, что с учетом исправления ошибок кратности t и меньше вероятность РНИ.³РНИ.ДОП.

Задача 3.4 решается вполне аналогично. Необходимо только иметь в виду, что здесь для уменьшения вероятности предъявления получателю сообщения с незамеченной ошибкой РОШ. мы заинтересованы в повышении кратности r обнаруживаемых ошибок. Исправление ошибок эту вероятность не уменьшит. Для обнаружения ошибок кратности r и меньше понадобится (n,k) - код с расстоянием d0³(r+1). Быть может, требованиям задачи удовлетворяет код с расстоянием d0=2 (с четным весом). Если это не так, можно для определения числа контрольных символов (n–k) воспользоваться выражением (3.5).

Наконец, рассмотрим еще решение задачи 3.6, так как она отличается от всех других двумя факторами:

1. Здесь сообщение («отсчет» измеряемой аналоговой величины) отображается не одним кодовым словом, а последовательностью (массивом) из трех слов.

2. Для передачи кодовых слов используется асимметричный двоичный канал, в котором Р1–0 ¹Р0–1.

На рис.3.1 представлены диаграммы сигналов для данного случая. Каждый отсчет измеряемой величины представлен в двоичном канале как последовательность трех десятичных цифр, каждая из которых, в свою очередь, отображается словом кода с постоянным весом, например, кодом «2 из 5». Ниже приведен вариант такого отображения.

0 – 11000 2 – 10010 4 – 01100 6 – 01001 8 – 00101

1 – 10100 3 – 10001 5 – 01010 7 – 00110 9 – 00011

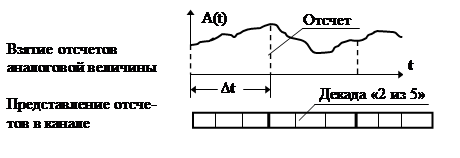
Рис. 3.1. Диаграмма сигналов к задаче 3.6

Требуется вычислить:

РНИ - вероятность предъявления получателю неискаженного отсчета (сообщения).

РОШ - вероятность предъявления отсчета с незамеченной ошибкой.

По-видимому, следует начать с нахождения аналогичных вероятностей для одной декады.

По условию задачи вероятности ложного опознавания бит Р1–0, и Р0–1 являются константами, которые не зависят от времени, от размещения бит в кодовом слове. Следовательно, для нахождения вероятности можно оперировать некоторым «стандартным форматом», каким является, например, отображение цифры 0 или 9. Здесь компактно расположены w символов «1» и (n – w) символов «0». Тогда:

1. По теореме о вероятности совместного наступления независимых событий вероятность получения неискаженной декады

 Скачать реферат