Несобственные интегралы

Доказательство. Рассмотрим вспомогательную функцию . Очевидно, что она удовлетворяет неравенствам . Согласно теореме 1 из сходимости 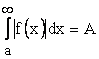следует сходимость . Но тогда 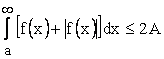и 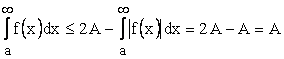. Следовательно, несобственный интеграл 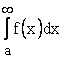сходится, что и требовалось доказать.

Аналогичная теорема имеет место и для несобственных интегралов от разрывных функций.

Теорема 4. Если положительные функции и непрерывны на промежутке и при этом , то оба несобственных интеграла 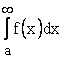и 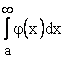ведут себя одинаково.

Данную теорему доказывать не будем. Аналогичная теорема существует и для несобственных интегралов от разрывных функций, но при вычислении предела переменная стремится к точке разрыва.

В заключение отметим, что в качестве известных или эталонных функций, упоминаемых в теоремах, часто используются функции и 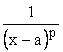проинтегрированные в примерах параграфов 15 и 1

Литература

1. Бугров Я.С., Никольский С.М. ВЫСШАЯ МАТЕМАТИКА В 3-х томах Т. 1 Элементы линейной алгебры и аналитической геометрии 8-е изд. Изд-во: ДРОФА, 2006. – 284 с.

2. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М., «Наука», 1986.

3. Лобоцкая Н.Л. Основы высшей математики. Минск, «Высшая школа», 1973.

4. Минорский В.П. Сборник задач по высшей математики.

5. Мироненко Е.С. Высшая математика. М: Высшая школа, 2002. – 109 с.

6. Никольский С.М., Бугров Я.С. ВЫСШАЯ МАТЕМАТИКА В 3-Х ТОМАХ Т. 2 Дифференциальное и интегральное исчисление 8-е изд. Изд-во: ДРОФА, 2007. – 509 с.

7. Олейник С.Н. Математический анализ в задачах и упражнениях. Несобственные интегралы и ряды Фурье. Изд-во: Факториал Пресс, 1998. – 488c.

8. Черненко В.Д. Высшая математика в примерах и задачах. В трех томах. ПОЛИТЕХНИКА, 2003.

 Скачать реферат