Линейные диофантовые уравнения

Поскольку первый автобус стартует из пункта А, к моменту n-го визита в А он пройдет путь S’n = 4(n-1) (последовательность S'n образует арифметическую прогрессию с разностью 4).

Поэтому

T’n=.

Второй автобус к моменту n-го визита в А пройдет путь S”n= 2 + 4(n -1) = 4n - 2 (последовательность S”n также будет арифмети

ческой прогрессией с разностью 4). Поэтому T”n=.

Встреча автобусов в пункте А означает, что для некоторых нату­ральных n и т верно равенство

T’n= T”n28n-34m=11

Левая часть этого уравнения — четное число, а правая — нет. Поэтому оно не имеет решений в целых числах. Следовательно, автобусы никогда не встретятся в пункте А.

Теперь перейдем непосредственно к решению второй части за­дачи. Для этого введем систему координат на дороге между А и В, выбрав в качестве начала отсчета пункт А, в качестве положитель­ного направления — направление от А к В (рис. 2).

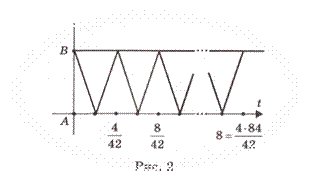
Пусть x1(t), x2(t) — координаты первого и второго автобусов соот­ветственно в момент t. Графики функций x1(t) и x2(t) — это ломаные линии, изображенные на рисунках 1 и 2 соответственно. Первая ломаная состоит из 102 пар звеньев с угловыми коэффициентами 51 и -51, а вторая — из 84 пар звеньев с угловыми коэффициентами 42 и -42 (на рисунках мы исказили масштаб). Точки А и В на оси ординат имеют координаты 0 и 2 соответственно и соответствуют прохождению через пункты А и В.

Встреча автобусов в какой-то момент t означает совпадение их координат в этот момент: x1(t) = x2(t), то есть пересечение графиков функций x1(t) и x2(t).

Каждое звено первой ломаной пересекает вторую ломаную ровно в одной точке. Поэтому всего будет 102 точки пересечения возрас­тающих звеньев первой ломаной со второй ломаной и 102 точки пе­ресечения убывающих звеньев первой ломаной со второй ломаной. Поскольку автобусы не встречаются в пункте А, ни одна из этих точек не будет лежать на оси абсцисс. С другой стороны, поскольку авто­бусы встречаются 6 раз в пункте В, ровно 6 точек пересечения будет лежать на горизонтальной прямой у = 2. Эти точки будут включены как в 102 точки пересечения возрастающих звеньев первой ломаной со второй ломаной, так и в 102 точки пересечения убывающих звеньев первой ломаной со второй ломаной. Поэтому число точек пересече­ния, лежащих внутри полосы 0 < у < 2, равно

2•(102-6)=192

Ответ: а) 6 раз; б) 192 раза.

 Скачать реферат