Линейные диофантовые уравнения

Поскольку число копеек не может быть больше, чем 99, справед­ливо двойное неравенство: 1 ≤ n, m ≤ 99. Оно, в частности, влечет, что сдача не превышает первоначальную сумму в 100 рублей, которая была у Темы.

Хотя уравнение (8) является стандартным уравнением в целых числах вида ах + by = с, найти его частное решение (чтобы свести дело к однородному уравнению) простым подбором вес

ьма непро­сто. На этом примере мы продемонстрируем общий метод поиска частного решения (алгоритм Евклида), который автоматически приводит к успеху.

Рассмотрим коэффициенты при неизвестных (а = 97 и b = 299) и разделим больший коэффициент на меньший. В результате получим неполное частное 3 и остаток 8. Иначе говоря, справедливо равен­ство 299 = 3•97 + 8, или, что то же самое, 8 = 299 -3•97.

Теперь заменим больший коэффициент (то есть 299) на остаток (то есть 8) и проделаем с парой 97, 8 ту же процедуру: разделим 97 на 8. В результате мы получим неполное частное 12 и остаток 1. Иначе говоря, справедливо равенство 97 = 12•8 + 1, или, что то же самое, 1 = 97 — 12•8. Заменим в этом равенстве число 8 выражением 299 – 3 • 97, найденным в предыдущем абзаце:

1 = 97-12• (299 – 3 • 97) = 37 • 97 – 12 • 299.

Итак, мы представили число 1 (это наибольший общий делитель чисел 97 и 299) в виде линейной комбинации чисел 97 и 299. Ум­ножая последнее равенство на 140, мы получим искомое частное решение уравнения (8): т0 = 37 • 140 = 5180, п0 = 12 • 140 = 1680.

Это частное решение обычным образом приводит к следующему общему решению уравнения (8) в целых числах:

Условия 1 < n, т ≤99 однозначно определяют значение пара­метра k: k = -17, что приводит к следующим значениям основных неизвестных n и m=31, m=97.

Поэтому стоимость всех покупок Темы (в рублях) равна

100-31,97+1,40 = 69,43.

Проблему с поиском частного решения можно обойти с помощью следующего способа решения уравнения (8) (этот метод работает для любого уравнения вида ах+by=с и в сущности является вариантом алгоритма Евклида).

Выразим неизвестную с меньшим коэффициентом (в нашем случае — это т) через другую неизвестную:

И выделим целую часть из дробей , ,

Введем новую неизвестную т1 (вместо т) по формуле т1 = т - Зn -1. Для нее последнее равенство примет вид:

97m1 = 8n + 43.

Это уравнение имеет тот же вид, что и исходное. Применим к нему процедуру, описанную в предыдущем абзаце: выразим неиз­вестную с меньшим коэффициентом (в нашем случае — это n) через другую неизвестную:

и выделим целую часть из дробей ,

Введем новую переменную n1 (вместо n) по формуле n1 = n1 - 12т1 + 5. Для нее последнее равенство примет вид:

8n1 = т1-3.

Поскольку коэффициент при т1 равен 1, общее решение этого уравнения в целых числах есть:

.

Возвращаясь к основным неизвестным /гит, мы получим общее решение в целых числах уравнения (8)

При l=k+17 мы получим общее решение уравнения (8), най­денное ранее.

Описанный метод решения линейных диофантовых уравнений был известен уже математикам Древней Индии; они называли его «метод рассеивания».

Ответ: 69 руб. 43 коп.

Задача 7. Длина дороги, соединяющей пункты А и В, равна 2 км. По этой дороге курсируют два автобуса. Достигнув пункта А или пункта В, каждый из автобусов немедленно разворачивается и следует без остановок к другому пункту. Первый автобус движется со скоростью 51 км/ч, а второй — со скоростью 42 км/ч. Сколько раз за 8 часов движения автобусы

а) встретятся в пункте В;

б) окажутся в одном месте строго между пунктами А и В,

если известно» что первый стартует из пункта А, а второй — из пункта В?

Решение. Примем момент старта автобусов в качестве начального

и обозначим через t'n , t’n моменты времени, когда первый и второй автобусы в n-й раз окажутся в пункте В.

Поскольку первый автобус стартует из пункта А, к моменту n-го визита в В он пройдет путь sп = 2 + 4(n -1) = 4n - 2 (последователь­ность s’n образует арифметическую прогрессию с разностью 4).

Поэтому t’n= .

Второй автобус к моменту n-визита в пункт В пройдет путь s’n = 4(n-1) = 4n -4 (последовательность s’n также будет арифметической прогрессией с разностью 4). Поэтому t’n =.

Встреча автобусов в пункте В означает, что для некоторых нату­ральных n и т верно равенство

T’n= T’m14n-17m=-10

Рассмотрим его как уравнение относительно п и т и решим его.

В качестве частного решения можно взять, например, n0 = 9, m0 = 8:

14•9-17•8 = -10.

Вычитая это равенство из уравнения 14n — 17m = -10, мы полу­чим однородное уравнение:

14(n-9) = 17(m-8).

Его общее решение в целых числах имеет вид: n - 9 = 17k, т - 8 = 14k, где k Z. Отсюда

n = 9 + 17k, m = 8 + 14k. Поскольку нас интересует решение в натуральных числах, возможные значения целочислен­ного параметра k должны быть неотрицательными: k Z . Пере­менную k можно интерпретировать как номер встречи автобусов в пункте В (имея в виду, что встречи нумеруются не с 1, а с 0). Момент k-й встречи можно подсчитать как t’n при n = 9 + 17k: tk = .

Число встреч за 8 часов равно числу решений неравенства tk ≤ 8 на множестве k Z:

Таким образом, за 8 часов автобусы ровно 6 раз встретятся в пункте В.

Перейдем теперь ко второй части задачи («сколько раз за 8 часов автобусы окажутся в одном месте строго между пунктами А и В? »). Прежде всего найдем, сколько раз за 8 часов автобусы встретятся в пункте А — эта информация окажется позже нам полезной.

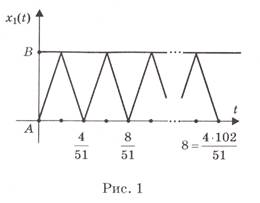
Как и в предыдущем исследовании, примем момент старта авто­бусов в качестве начального и обозначим через T’n, T"n — моменты времени, когда первый и второй автобусы в n-й раз окажутся в пункте-А (рис. 1).

 Скачать реферат