Линейные пространства

Значительное место в теории векторных пространств занимает теория линейных преобразований векторного пространства. Пусть – два векторных пространства над одним и тем же полем К. Линейным отображением, или линейным оператором, Т, отображающим векторное пространство в векторном пространстве (или линейным оператором из в .

Два векторных пространства и называются изоморфными векторными пространствами, если существует линейный оператор («изоморфизм»), осуществляющий взаимно однозначное соответствие между их элементами и .

С теорией линейных отображений векторного пространства тесно связана теория билинейных отображений и полилинейных отображений векторного пространства.

Важную группу задач теории векторного пространства образуют задачи продолжения линейных отображений. Пусть F – подпространство векторного пространства – линейное пространство над тем же полем, что и , и пусть – линейное отображение F в ; требуется найти продолжение Т отображения , определенное на всем и являющееся линейным отображением в . Такое продолжение всегда существует, но дополнительные ограничения на функции (связанные с дополнительными структурами в векторное пространство, например, топологией или отношением порядка) могут сделать задачу неразрешимой. Примерами решения задачи продолжения являются Хана–Банаха теорема и теоремы о продолжении положительных функционалов в пространствах с конусом.

Важным разделом теории Векторных пространств является теория операция над векторными пространствами, т.е. способов построения новых векторных пространств по известным. Примеры таких операций – известные операции взятия подпространства и образования факторпространства по подпространству. Другие важные операции – построение прямой суммы, прямого произведения и тензорного произведения векторного пространства.

Базис и размерность линейного пространства

Будем далее полагать, что на множестве значений интересующих нас свойств точки объекта введена структура векторного пространства. Обозначим такое векторное пространство через V. Совокупность свойств f есть вектор (точка, элемент) этого пространства: .

Если нас интересует одно свойство f физического тела, то множество V таково, что для сопоставления f числа достаточно выбрать один базисный элемент (базисный вектор) e с эталонным значением этого свойства. Этому значению ставится в соответствие число 1, а остальным значениям f – другие числа в соответствии с формулой . Такая связь называется линейной.

В общем случае число базисных элементов должно равняться числу изучаемых свойств тела. Легко показать, что для того, чтобы однозначно связать независимых друг от друга свойств с числами требуется n эталонов, т.е. совокупность базисных векторов. Числовой характеристикой совокупности свойств в каждой точке тела будет упорядоченная совокупность n чисел. (1)

Введение структуры векторного пространства на множестве приводит к тому, что все элементы множества оказываются связанными друг с другом соотношениями вида

(2.2)

где – числа, а – векторы. Сумма, стоящая в левой части равенства (2.2) называется линейной комбинацией векторов f, g, h, …. На этом, в частности, и основано сопоставление вектору f совокупности чисел (): каждый элемент множества записывается в виде линейной комбинации базисных векторов

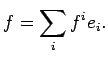(2.3)

Основная задача базисных векторов (т.е. эталонных элементов) – обеспечивать взаимнооднозначную связь векторов (в том числе и самих себя) с совокупностями характеризующих их чисел. Какие ограничения накладывает это требование на выбор базисных векторов?

Допустим, свойства f характеризуются эталонами неоднозначно, т.е. существует два (или более) разных набора чисел и {} таких, что

(2.4)

и имеется хотя бы одно значение i=k, при котором . В этом случае разность представлений (2.4) такова

(2.5)

и хотя бы для одного значения индекса i=k коэффициент . Тогда значение k-го эталона может быть выражено через значения остальных эталонов

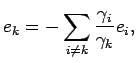(2.6)

и это говорит о том, что эталоны являются зависимыми друг от друга, точнее – линейно зависимыми, так как связь (2.6) является линейной.

Очевидно, для обеспечения указанной однозначности описания совокупность эталонов, т.е. базисных векторов, должна быть линейно независимой. Это значит, что равенство (2.5) должно выполняться лишь в том случае, когда все коэффициенты , т.е. , для всех i. Отсюда же следует, что если базисные векторы линейно независимы, нулевому вектору всегда ставится в соответствие совокупность чисел, состоящая из одних нулей.

Если при описании совокупности независимых свойств использовать m<n базисных векторов, то описать все векторы из V линейными комбинациями (2.3) не удастся. Если для описания элементов V суммами (2.3) воспользоваться p>n базисными векторами, мы утратим единственность описания. Таким образом, существует некоторое минимально необходимое число базисных векторов n, которое называется размерностью векторного пространства.

 Скачать реферат